A cube and a pyramid

Geometry Level 4

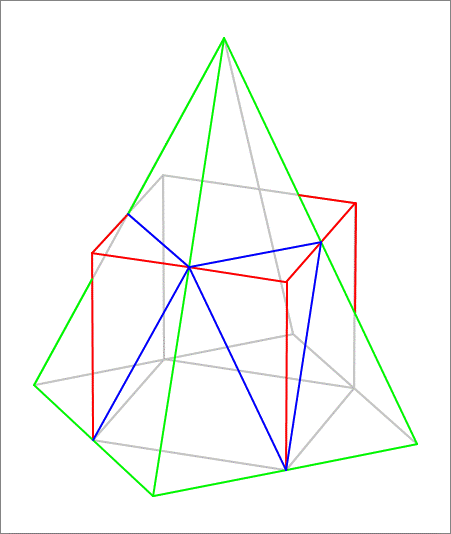
A cube of side length 10 10 has a right square pyramid intersecting with it as shown in the figure, below, where the vertices of the cube base are the midpoints of the sides of the square base of the pyramid. In addition, the height of the pyramid is such that the slant edges of the pyramid pass through the midpoints of the upper edges of the cube. Find the volume of the pyramid that is outside the cube.


The answer is 500.

Hosam Hajjir by Hosam Hajjir , 56, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Due to symmetry, we find that the four right-triangle-base pyramids (shaded) protruding out of the cube are identical. And two of these pyramid equal to the top square-base pyramid (shaded). And that the volume of the 4 4 side pyramids plus the volume of the top pyramid is the volume of the pyramid outside the cube or volume of the pyramid outside the cube V o V_o is equal to three times the volume of the top pyramid V t V_t or V o = 3 V t V_o = 3V_t . Since the top pyramid has a square base of side length 5 2 5\sqrt 2 and a height of 10 10 , V o = 3 × 1 3 ( 5 2 ) 2 × 10 = 500 V_o = 3 \times \frac 13 (5\sqrt 2)^2 \times 10 = \boxed{500} .

2 Helpful 1 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...