A Cube and an Octahedron
A cube of edge length 1, and an octahedron of edge length 1.5 share the same center, and are oriented such that all vertices of the octahedron lie on the normals to the faces of the cube drawn from the cube's 6 face centers, as shown in the figure below. Find the volume of this composite 3D figure.
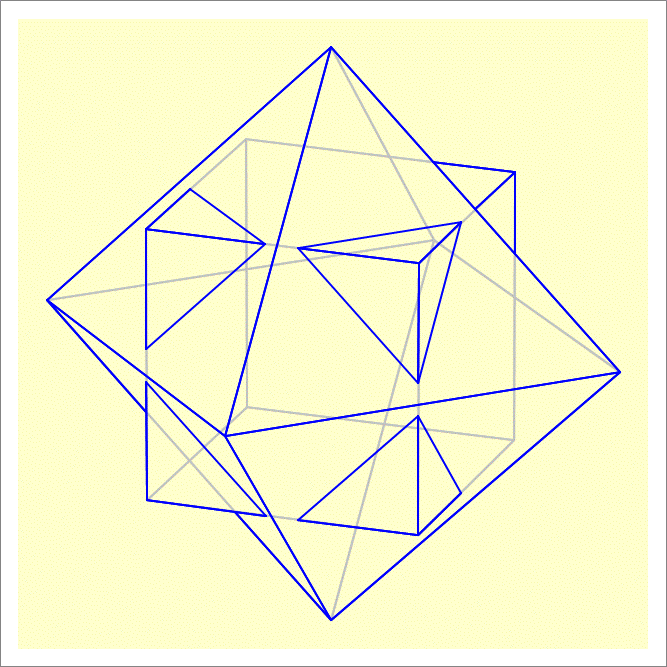
The answer is 1.704.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The volume of the composite 3D figure is given by V = V o + 8 V p , where V o is the volume of the octahedron and V p is the volume of one of the pyramids of the corners of cube.
Let the shared center of the cube and octahedron be the origin O ( 0 , 0 , 0 ) . The x - and y -axes is each perpendicular to a horizontal edge of the octahedron and the z -axis is vertical and passes through the top vertex of the octahedron A .
The top-half of the octahedron has a 2 3 × 2 3 square base, whose diagonals are 2 3 2 , and an altitude A O = ( 2 3 ) 2 − ( 4 3 2 ) 2 = 4 3 2 . Then it volume is V o = 2 × 3 1 ( 2 3 ) 2 A O = 8 9 2 .
Let us look at the 3D figure along the x -axis. Then the intercept of y -axis by its perpendicular horizontal octahedron edge is B ( 0 , 4 3 , 0 ) . The straight line A B is given by y − 4 3 z − 0 = − 4 3 4 3 2 ⟹ z = 4 3 2 − 2 y . We note that the top-right vertex of cube is D ( 0 , 2 1 , 2 1 ) . Then C ( 0 , y c , 2 1 ) and E ( 0 , 2 1 , z e ) . And 2 1 = 4 3 2 − 2 y c , ⟹ y c = 4 3 − 2 and z e = 4 3 2 − 2 × 2 1 = 4 3 2 − 4 . Let C D = a and D E = b . Then a = y d − y c = 2 1 − 4 3 − 2 = 4 3 2 − 3 and b = d e − z e = 2 1 − 4 3 2 − 4 = 4 6 − 3 2 .
Now, we note that the inverted pyramid of vertex D has a isosceles right triangle base with a hypotenuse of 2 a and a height of b . Therefore V p = 3 1 × a 2 × b = 6 4 9 0 − 6 3 2 .
Therefore V = V o + 8 V p = 8 9 2 + 8 × 6 4 9 0 − 6 3 2 = 8 9 0 − 5 4 2 ≈ 1 . 7 0 4 .