A cube inscribed in a cube
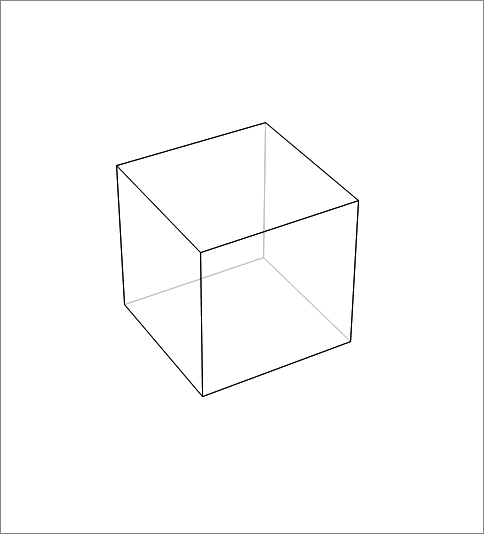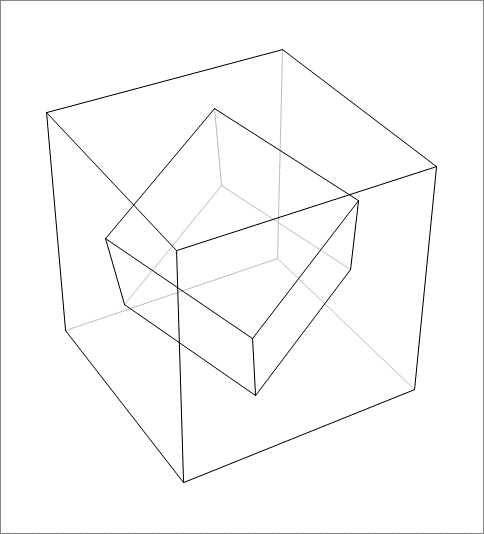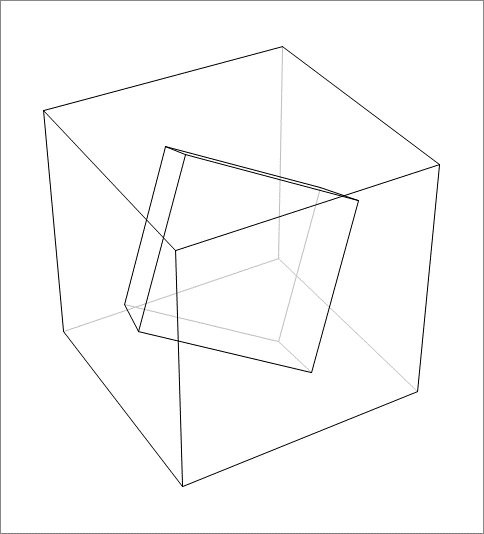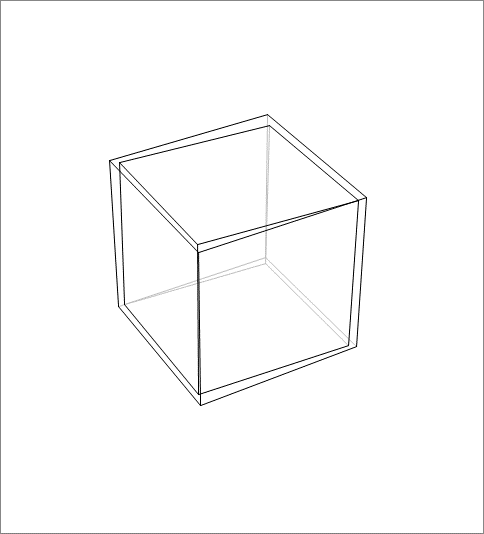
A unit cube centered at the origin has its 6 faces parallel to the coordinate planes. It starts rotating about its main diagonal which is along the vector ( 1 , 1 , 1 ) . The rotating cube can be inscribed in a bigger cube whose faces are parallel to the the coordinate planes. This is shown in the above animation. Find the maximum side length of the bigger cube, throughout the rotation of the unit cube. If the answer is of the form q p for positive coprime integers p and q , find p + q .
Note: 6 out of 8 vertices of the rotating cube will lie on the six faces of the outer cube, while the other 2 are fixed in place inside it.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the side length of the smaller rotating cube be 2 a . Then for our unit cube, a = 2 1 . The fixed vertices of the rotating cube are at ( a , a , a ) and ( − a , − a , − a ) . Now let's take the vertex ( a , a , − a ) and see its position after a rotation by θ .
The rotation matrix about the unit axis u = 3 1 ( 1 , 1 , 1 ) passing through the origin is
R ( θ ) = u u T + ( I − u u T ) cos θ + S u sin θ
where the matrix S u is given by
S u = ⎣ ⎡ 0 u z − u y − u z 0 u x u y − u x 0 ⎦ ⎤
Hence,
R ( θ ) = 3 1 ⎣ ⎡ 1 1 1 1 1 1 1 1 1 ⎦ ⎤ + 3 1 cos θ ⎣ ⎡ 2 − 1 − 1 − 1 2 − 1 − 1 − 1 2 ⎦ ⎤ + 3 1 sin θ ⎣ ⎡ 0 1 − 1 − 1 0 1 1 − 1 0 ⎦ ⎤
Hence the image of the vector p = ( a , a , − a ) is
p ′ = R ( θ ) p = a ( 3 1 ( 1 , 1 , 1 ) + 3 1 cos θ ( 2 , 2 , − 4 ) + 3 1 sin θ ( − 2 , 2 , 0 ) )
We can take any of the three coordinates of point p ′ and maximize it. Let's take p ′ y :
p ′ y = 3 a ( 1 + 2 cos θ + 2 3 sin θ )
The maximum of this combination of cos θ and sin θ is
Max ( p ′ y ) = 3 a ( 1 + 2 2 + ( 2 3 ) 2 ) = a ( 3 5 )
Thus the maximum side length is 2 a ( 3 5 ) = 3 5 , which makes the answer 5 + 3 = 8 .
Let O ( 0 , 0 , 0 ) be the center of both cubes, so that one of the fixed points on the rotating cube is A ( 2 1 , 2 1 , 2 1 ) .
Let N ( n , n , n ) be the center of the circle that B ( − 2 1 , 2 1 , 2 1 ) rotates around. Then O N = ( n , n , n ) and B N = ( n + 2 1 , n − 2 1 , n − 2 1 ) , and since O N ⊥ B N , n ( n + 2 1 ) + n ( n − 2 1 ) + n ( n − 2 1 ) = 0 , which simplifies to n = 6 1 .
Let C ( a , b , c ) be the locus of points of B rotating around N . Then O N = ( 6 1 , 6 1 , 6 1 ) and C N = ( 6 1 − a , 6 1 − b , 6 1 − c ) , and since O N ⊥ C N , 6 1 ( 6 1 − a ) + 6 1 ( 6 1 − b ) + 6 1 ( 6 1 − c ) = 0 , which simplifies to c − 2 1 = a + b .
Also, A C = 1 , so by the distance equation ( a − 2 1 ) 2 + ( b − 2 1 ) 2 + ( c − 2 1 ) 2 = 1 . Substituting c − 2 1 = a + b gives ( a − 2 1 ) 2 + ( b − 2 1 ) 2 + ( a + b ) 2 = 1 , an equation of an ellipse, which rearranges to b = 4 1 ( − 2 a + 1 ± − 1 2 a 2 + 4 a + 5 ) and has maximum and minimum a -values when the discriminant − 1 2 a 2 + 4 a + 5 = ( 2 a + 1 ) ( − 6 a + 5 ) = 0 , so that the minimum is a = − 2 1 and the maximum is a = 6 5 .
a = 6 5 also represents the maximum of half the side length of the larger cube, so the maximum full side length of the larger cube is s = 2 ⋅ 6 5 = 3 5 , which means p = 5 , q = 3 , and p + q = 8 .