A cubic polynomial

Put $g(x)=p(x) - x$ which is a polynomial of degree 3 and vanishes at 1,2 and 3. Thus $g(x)=A(x-1)(x-2)(x-3)$ Since $g(4)=A(4-1)(4-2)(4-3)=1$ So $A=1/6$ . Thus $p(x)=x+g(x)=x + \frac { (x-1)\cdot (x-2)\cdot (x-3) }{ 6 }$ Hence $p(6)=16$ .

We can construct a difference table as follows: 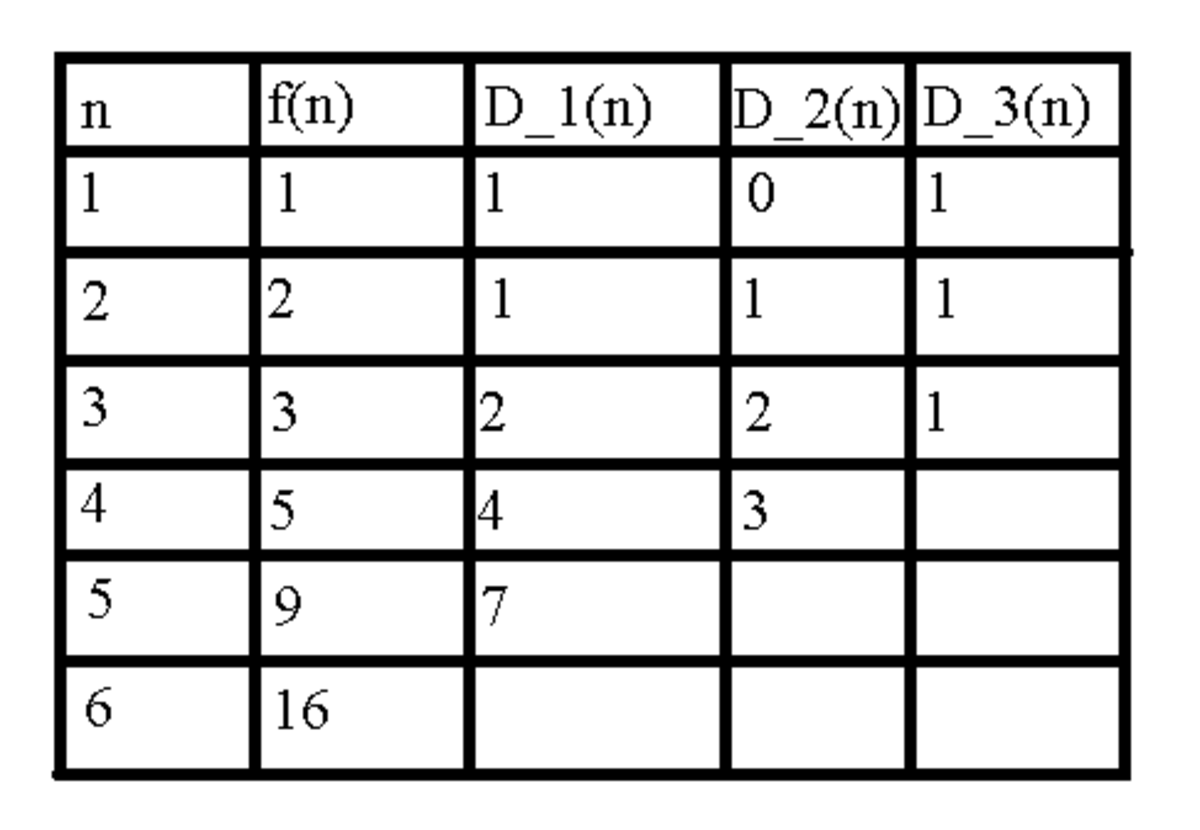For those who do not know what is a difference table,they should read the
Method Of Differences Wiki

I looked at $p(x)-x$ (as below) but the method of differences would also give the same result. Cubic functions have constant third differences.

$p(x)=ax^{3}+bx^{2}+cx+d$ Plugging in values of $x$ , we get a system of linear equations $p(1)=a+b+c+d=1$ $p(2)=8a+4b+2c+d=2$ $p(3)=27a+9b+3c+d=3$ $p(4)=64a+16b+4c+d=5$ Solving the system of linear equations give $a=\frac{1}{6}$ $b=-1$ $c=\frac{17}{6}$ $d=-1$ So $p(6)= \frac{1}{6}(6^{3})-6^{2}+\frac{17}{6}(6)-1=\boxed{16}$