A Cubic Resistance.
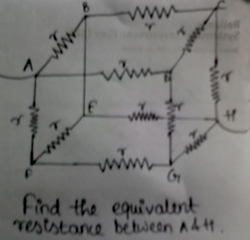 Find the Equivalent resistance of the cube between A and H from the given diagram.If r=1.
Find the Equivalent resistance of the cube between A and H from the given diagram.If r=1.
The answer is 0.833.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The points F,D & B are at same potential hence they can be added together such that resistances AB,AD,AF ,becomes parallel . Similarly the points E,C& G .too are at same potential and they too can be joined .Hence we get a structure with a 6 resistances parallel and a pair of three resistances parallel.hence equivalent resistance is R e q = 3 r + 6 r + 3 r .Hence solving this we get R e q = 6 5 r hence putting the value of r we get R e q = 0 . 8 3 3 . . .
ARE "B" AND "E" NOT AT SAME POTENTIAL,sir
Log in to reply
They have the same potential indeed.What makes you disagree with that?!
Assume that 3 i current enters the circuit .Now we know that the resistance being the same through out, the current will divide equally as i at first and then as i/2 (at B,F and D).Now these will combine to give current i (at G,E and C) and as 3 i at H. Now we get ,1.V(A) - V(D)=i r (Applying V=I R). 2.V(D) - V(G)=i/2 r. 3.V(G) - V(H)=i r. Hence we get ,
V(A) - V(H)=i r+i/2 r+i r=5/2 i*r.
IF Equivalent resistance is assumed to be R,
Then ,we get V(A) - V(H) = 3 i R.
or ,3 i R=5/2 i r.
R = 5/6*r.(Here r=1).So R=5/6=0.83.
Here V(A) - V(D) means Potential difference across A and D.
Vaibhav First sketch it correctly
Dude you mustn't just copy-paste the NCERT solution. You must edit it such that it suits the question
To be honest i am not having any NCERT book.
Log in to reply
Where did you get this form then?
Log in to reply
From an old WBJEE Question set.WBJEE(West Bengal Joint Entrance Examination).
Divide the current and apply kirchoff's law to find the eq resistance.
Actually this question answers only when there is another resistor between B and E ..... only then does Vaibhav's solution goes right .