A Cubical grid

In this problem, we have to figure out what kind of cubes are allowed, and how many there are

Case 1: All the faces are parallel to the 3 planes.

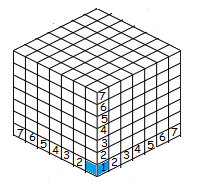
This is easy to deal with:
$7 \times 7 \times 7 = 343$ cubes of length 1,
$6 \times 6 \times 6 = 216$ cubes of length 2,
$5 \times 5 \times 5 = 125$ cubes of length 3,
$4 \times 4 \times 4 = 64$ cubes of length 4,
$3 \times 3 \times 3 = 27$ cubes of length 5,
$2 \times 2 \times 2 = 8$ cubes of length 6,
$1 \times 1 \times 1 = 1$ cubes of length 7.
Hence, there are 784 cubes here.

Case 2: Exactly 1 face is parallel to the plane.

Consider the face of the cube that is parallel to the plane.
We know that this face is a square.
Since the cube is not parallel to the other faces, this means that the edges of the square are not along the grid lines.
Thus, the sides of the square are "tilted" like the figure on the left.
The vertices are still on lattice points.

In addition, by considering the normal direction to the face, we get that the side length of the cube must be an integer. This means that the side length of the square is also an integer, so the 2 red squares would not work. If we consider the square grid that exactly encompasses the face, we get small right triangles that have integer lengths, aka a pythagorean triples . If we consider the 3-4-5 triangle, we get the following squares that just fit in:

Let is clear that there are no other Pythagorean triples that we can use, to place within the $8 \times 8$ grid,

Now, let's count the number of possible configurations in this case:
There are 3 possible faces to be parallel to (we chose the $x-y$ plane at the start).
For each plane, there are 2 possible arrangements of the square (red and blue above).
Since the height of the cube is 5, the bottom face of the cube could be at $z = 1, 2, 3$ .
Hence, there are $3 \times 2 \times 3 = 18$ possible cubes.

Conclusion: The total number of cubes are $784+18=802$