A Curious Observation

Relevant wiki: 2D Coordinate Geometry - Problem Solving

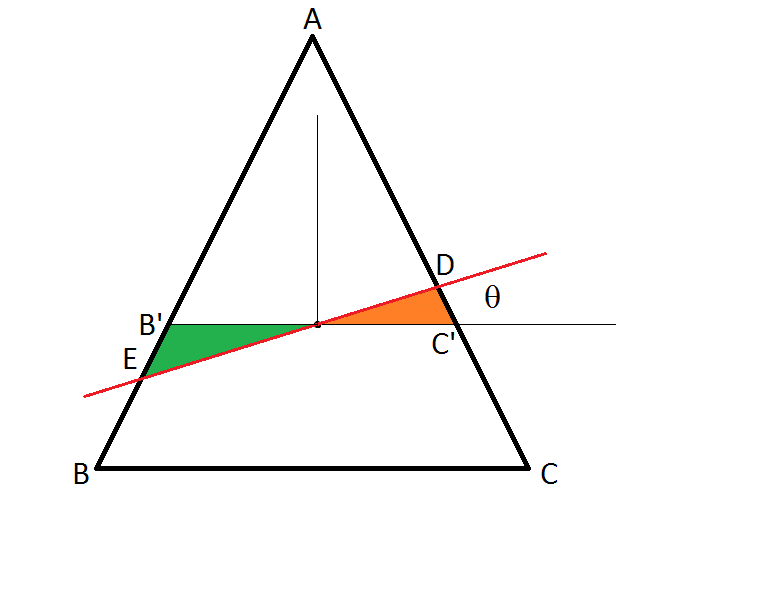
It can be easily seen that any triangle can be transformed into
an equilateral triangle by a linear transformation that preserves
the ratios of the areas within the two triangles.

So we'll work with an equilateral triangle (with side length equal to 1). As the figure shows, the dividing line intersects AC at D and AB at E, Let the origin of the coordinate frame be at the centroid, and let the
line make an angle $\theta$ with the x-axis.

The coordinate of $A = (2/3) \sqrt{3} / 2 = \sqrt{3} / 3$

Hence, the line AB has the equation:
$y = \sqrt{3} / 3 + \sqrt{3} x$

and line AC has the equation
$y = \sqrt{3} / 3 - \sqrt{3} x$

and the equation of the cutting line is
$y = (tan \theta) x$

Let's find the $y$ -coordinates of $D$ and $E$ .

For point $D$ ,
$x_D = (\sqrt{3} / 3) /( \tan \theta + \sqrt{3} )$
therefore,
$y_D = \sqrt{3} \tan \theta / 3 ( \tan \theta + \sqrt{3} )$

and for point E, one can show that
$y_E = \sqrt{3} \tan \theta / 3 ( \tan \theta - \sqrt{3} )$

Note that because of symmetry considerations, we're interested only
in values of $\theta$ between 0 and $\pi / 6$ .

Since the absolute value of $y_E$ is greater than the absolute value of $y_D$ ,
the green triangle in the figure is greater in area than the orange
triangle. This implies that the area of triangle AED can only increase
from the original position with $\theta = 0$ . The maximum area is
obtained when $\theta = \pi / 6$ . At which point trianlge AED will be
half the area of triangle ABC.

Therefore the minimum ratio is obtained with $\theta = 0$ .
At that position, AED is similar to ABC, the ratio of the sides being
$2/3$ , hence the ratio of the areas will be $4/ 9$
This means that the ratio of smaller portion to the larger portion will be
$4 / 5 = 0.8$ .

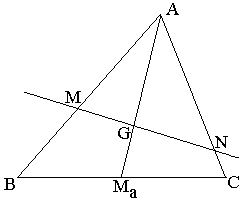
If $G$ is the centroid of triangle $ABC$ and the line passing through $G$ intersects $BA$ at $M$ and $CA$ at $N$ , then $\frac{BM}{MA} + \frac{CN}{NA} = 1$ . See A Characteristic Property of Centroid for proof.

Let $BM$ be $a$ , $MA$ be $b$ , $CN$ be $c$ , $NA$ be $d$ . Then, $\frac{a}{b} + \frac{c}{d} = 1$ .

The area of the smaller region is $\frac{1}{2} \sin(\angle BAC) bd$ while the larger region has area $\frac{1}{2} \sin(\angle BAC) [(a+b)(c+d)-bd]$ .

We want to minimize $\frac{\frac{1}{2} \sin(\angle BAC) bd}{\frac{1}{2} \sin(\angle BAC) [(a+b)(c+d)-bd]} = \frac{bd}{(a+b)(c+d)-bd}$ .

This is equivalent to finding the maximum value of $\frac{(a+b)(c+d)-bd}{bd} = \frac{ac+ad+bc}{bd} = \frac{ac}{bd} + (\frac{a}{b} + \frac{c}{d}) = \frac{ac}{bd}+1$

To find the maximum value of $\frac{ac}{bd}$ , let $\frac{a}{b} = x$ and $\frac{c}{d} = y$ . By AM-GM, $\frac{x+y}{2} = \frac{1}{2} \geq \sqrt{xy}$ , so the maximum value of $\frac{ac}{bd} +1$ is $\frac{5}{4}$ .

The minimum value of $\frac{bd}{(a+b)(c+d)-bd}$ is $\boxed{0.8}$

Let the given triangle have area $1$ . Without loss of generality, assume that the line cuts through sides $AC$ and $BC$ at points $X$ and $Y$ respectively. Using barycentric coordinates, we label $X=(a,0,1-a), Y=(0,b,1-b), C=(0,0,1)$ and the centroid $G=(1,1,1)$ . Now it should be clear from the definition of the centroid that $\frac{1}{2}\leq a,b \leq 1$ . Since $X,Y,G$ are collinear, we know that $\det\begin{vmatrix} a & 0 & 1-a\\ 0 & b & 1-b\\ 1 & 1 & 1 \end{vmatrix}=0\Rightarrow 3ab-a+b=0 \Rightarrow b=\frac{a}{3a-1}$ and we know can find the area $T$ of triangle $XCY$ in terms of $a$ only: $T=\det\begin{vmatrix} a & 0 & 1-a\\ 0 & b & 1-b\\ 0 & 0 & 1 \end{vmatrix}=ab=\frac{a^2}{3a-1}=\frac{1}{3}.$ Treating $T$ as a function of $a$ , we find $T(\frac{1}{2})=T(1)=\frac{1}{2}.$ Also $T'(a)=\frac{a(3a-2)}{(1-3a)^2}$ , which is negative for $a\in [\frac{1}{2},\frac{2}{3})$ and positive for $a\in (\frac{2}{3},1]$ . So we know that triangle $XCY$ has the lesser or equal area out of the two divided regions. Lastly $T'(a)=0\Rightarrow a=\frac{2}{3}$ (note the domain defined at the start) which will correspond to the desired minimum ratio. Thus the minimum area is $\frac{4}{9}$ and the minimum ratio is $\frac{4}{5}$ .