A Curious Problem (2)

Similar solution with @Hollow Knight 's. Since it took me some time to prepare the figure, I must well present it.

Given that $\dfrac 1a + \dfrac 1b + \dfrac 1c + \dfrac 1d + \dfrac 1e = 1$ , where $a$ , $b$ , $c$ , $d$ , and $e$ are distinct positive integers, let us assume $a < b < c < d < e$ . Let the unit square represent the number $1$ (the right-hand side of the equation). We note that $a$ cannot be $1$ , otherwise the left-hand side will be larger than $1$ which is the right-hand side. Let $a = 2$ , halving the square; $b=4$ halving the half square, and $c=8$ halving the quarter square. Here, we cannot halve the eighth square because then we would have $d=e = 16$ . Instead we divide one eighth by three parts of $\frac 1{24}$ . Since $d < e$ , $\frac 1d = \frac 1{24} \times 2 = \frac 1{12} \implies d = 12$ and $e = 24$ .

So we have $\boxed{a=2, b=4, c = 8, d = 12, e = 24}$ .

I used process of elimination to solve this one.

The potential values of $a$ are 0, 1, and 2.

If $a=0$ - Zero is in the denominator, so that can't be right. (Eliminates the answer choice with a=0)

If $a=1$ - Then the equation will look like $\frac{1}{1} + … = 1$ . Since the rest of the variables are positive integers, this can't be true. (Eliminates the answer choice with a=1)

This leaves the two remaining answer choices, where $a=2$ .

Since we know for sure that the equation will look like: $\frac{1}{2} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d} + \frac{1}{e} = 1$ , we also know that:

$\frac{1}{b} + \frac{1}{c} + \frac{1}{d} + \frac{1}{e} = \frac{1}{2}$

Also, in both cases, $b=\frac{1}{4}$ . So we now know that:

$\frac{1}{c} + \frac{1}{d} + \frac{1}{e} = \frac{1}{2} - \frac{1}{4} = \frac{1}{4}$

The differences between the remaining two answer choices are the values of $c$ , $d$ , and $e$ :

$\text{(1) } c=6, d=36, e=12$

$\text{(2) } c=8, d=12, e=24$

So we just need to find which of the above integer sets make $\frac{1}{c} + \frac{1}{d} + \frac{1}{e} = \frac{1}{4}$ true.

It turns out that the correct set of integers is: $a=2,b=4,c=8, d=12, e=24$

Geometry would be useful in solving this question.

We start by drawing a unit square and dividing it in halves (or any other proportion) so we now have two halves of the original square. We leave one side as it is (area on right in the diagram) and go on dividing the left half in two...

... Which gives us 1/4 and 1/4. We retain the area on the top and further divide the bottom area of 1/4 unit into 1/8 and 1/8.

Now as we can divide the area in any proportion we like, the last 1/8 area on the bottom left is divided into ratio of 1:2 making it 1/24 and 1/12 .

The summation of all this areas has to be 1 , because all of them were created by dividing a square having an area one.

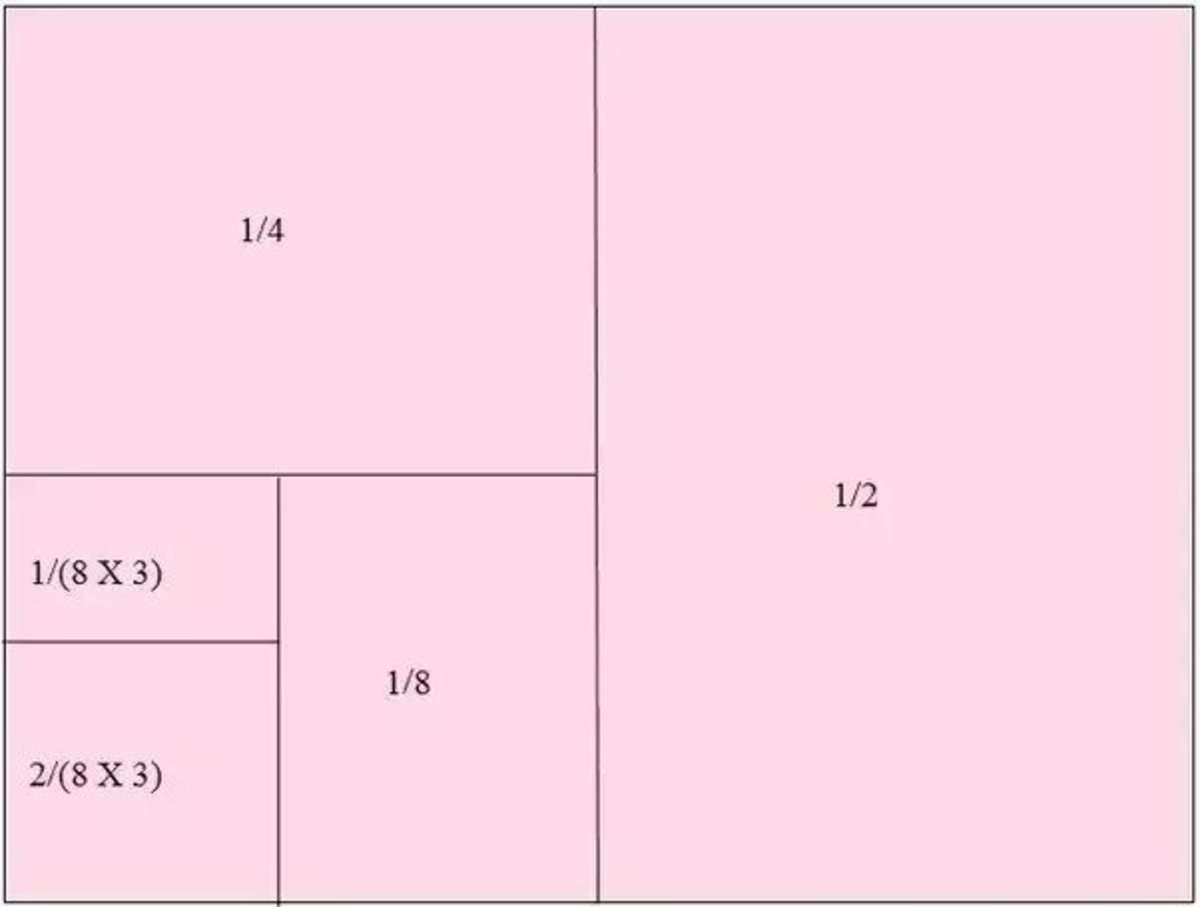
Therefore the answer is a = 2, b = 4, c = 8, d = 12 and e = 24.

Of course, other solutions can be generated here as well, such as a = 2, b = 4, c = 6, d = 36 and e = 18, which is similar to the last option here. (Whether that was intentional remains for you to decide.)