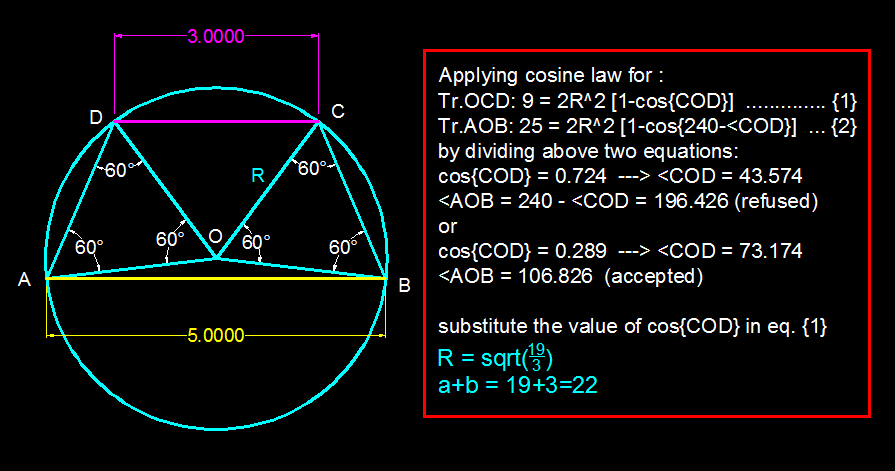
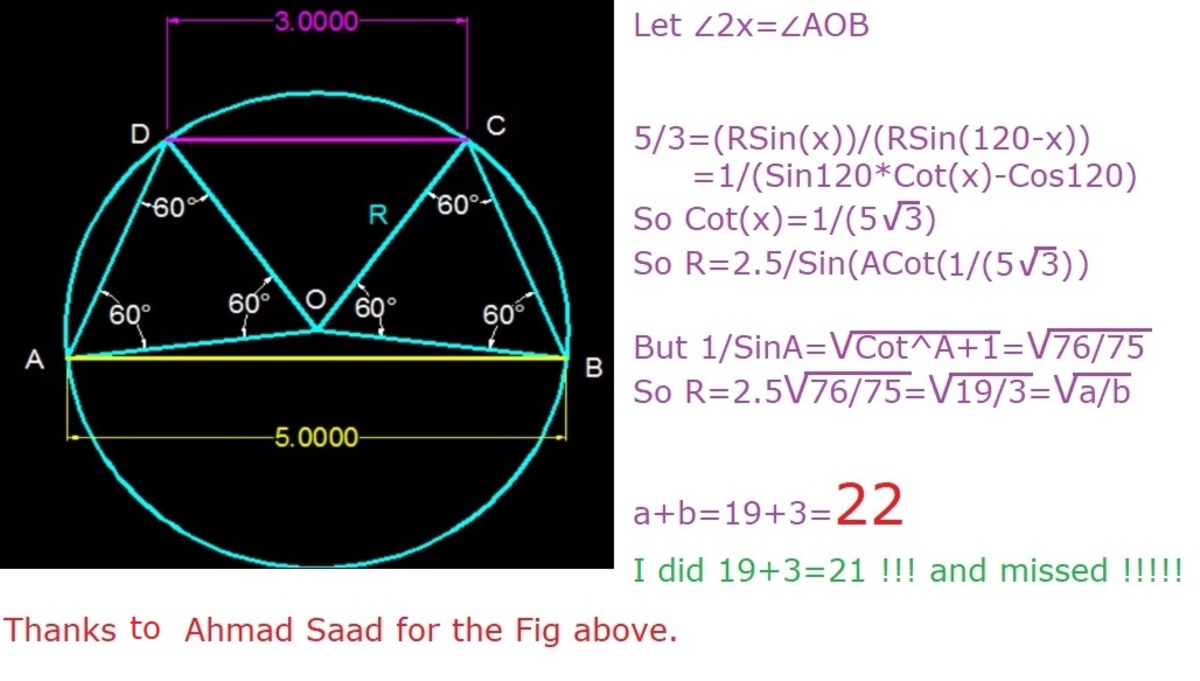
A Cyclic Trapezoid

Since $ABCD$ is cyclic, we can calculate the area as $A=\sqrt{(S-AB)(S-BC)(S-CD)(S-AD)}$ , where $S$ is the semi-perimeter. We can calculate $S=\frac{r+3+r+5}{2}=4+r$ , and substituting this into our area formula, we get $A=\sqrt{(r-1)(4)(r+1)(4)}=4\sqrt{r^2-1}$ .

Now let $O$ be the center of the circle, and draw a diameter through $O$ perpendicular to $AB$ and $CD$ . Let this diameter meet $AB$ and $CD$ at points $M$ and $N$ respectively. Because of symmetry, we also know that $M$ and $N$ are the midpoints of their respective sides. We can now use the basic formula for area of a trapezoid: $A=\frac{b_1+b_2}{2}h=4h$ . We also know (using right triangles): $h=MN=MO+NO=\sqrt{OA^2-AM^2}+\sqrt{OD^2-DN^2}=\sqrt{r^2-\frac{25}{4}}+\sqrt{r^2-\frac{9}{4}}$ .

Equating our areas, we solve for $r$ :

$4\sqrt{r^2-1}=4\Big( \sqrt{r^2-\frac{25}{4}}+\sqrt{r^2-\frac{9}{4}}\Big)$

$r^2-1=r^2-\frac{25}{4}+2\sqrt{\big( r^2-\frac{25}{4}\big) \big( r^2-\frac{9}{4}\big)}+r^2-\frac{9}{4}$

$15-2r^2=\sqrt{(4r^2-25)(4r^2-9)}$

$225-60r^2+4r^4=16r^4-136r^2+225$

$12r^4=76r^2$

$r^2=\frac{76}{12}=\frac{19}{3}$

$r=\boxed{\sqrt{\frac{19}{3}}}$ .