A dancing marble
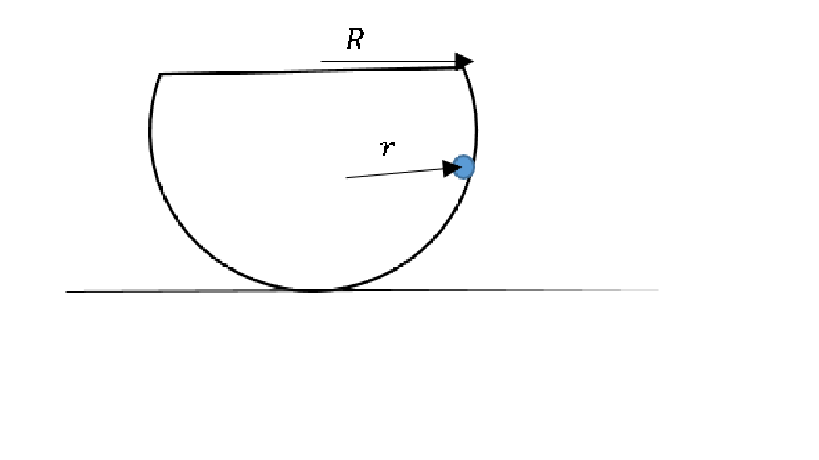 A massive hemispherical bowl of radius
is placed on the table as shown. A small marble is moving steadily in the bowl create a circular path in XY plane with radius
. If the marble is given a tiny kick so the marble has small z velocity component (parallel to the axis of the bowl). The angular frequency of small oscillation can be written as:
.
Find
when
.
Round your answer to 2 decimal places!
A massive hemispherical bowl of radius
is placed on the table as shown. A small marble is moving steadily in the bowl create a circular path in XY plane with radius
. If the marble is given a tiny kick so the marble has small z velocity component (parallel to the axis of the bowl). The angular frequency of small oscillation can be written as:
.
Find
when
.
Round your answer to 2 decimal places!
The answer is 1.07.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, consider the marble at equilibrium and use spherical coordinate. By Newton's second law we obtain
m ϕ 0 2 ˙ R cos θ = N cos θ 0 (1)...
m g = N sin θ 0 (2)...
Divide (1) and (2) we get
ϕ 0 2 ˙ = R sin θ 0 g (3)...
Now let's look at the motion of the marble after given a perturbation and again use spherical coordinate for convenience
The angular momentum of the system is conserved so we can write
m R 2 cos 2 θ 0 ϕ 0 ˙ = m R 2 cos 2 θ ϕ ˙
ϕ ˙ = ϕ 0 ˙ cos 2 θ cos 2 θ 0 (4)...
and the energy of the system is also conserved, given as
E = 2 1 m ( R 2 cos 2 θ ϕ 2 ˙ + R 2 θ 2 ˙ ) − m g R sin θ (5)...
Substitute eq (4) to (5) and then set the derivative of energy with respect to time equals zero due to energy conservation and using eq (3) we obtain
0 = sin θ 0 cos 3 θ g R cos 4 θ 0 sin θ + R 2 θ ¨ − g R cos θ
The particle is given a small kick in z-direction hence the small change in theta. Let's this change named as ϵ so according to Taylor expansion up to first order
sin θ ≈ sin θ 0 + ϵ cos θ 0
and
cos θ ≈ cos θ 0 − ϵ sin θ 0
This simplifies equation to (maintaining the first order of ϵ only)
0 = ϵ ¨ + R g ( 4 sin θ 0 + cot θ 0 cos θ 0 ) ϵ
So, the angular frequency is given by
ω = R g 4 sin θ 0 + cot θ 0 cos θ 0
Plug in r = 0 . 5 R we get
F ( r = 0 . 5 R ) = 2 3 + 6 3 = 1 . 9 4