A Described Quandary of an Inscribed Quadrilateral
If A B C D is an inscribed quadrilateral in a circle such that A B and C D extend to meet at E , A D and B C extend to meet at F , A B < C D , A D < B C , ∠ E = ∠ F , A B = 7 , the perimeter of △ A B F is 2 8 , and the perimeter of △ A D E is 1 2 , then find the area of A B C D .
The answer is 48.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
If I made the triangle ABF to be the largest one, I get 23.04. How do I know where do the alphabets go on that quadrilateral?
Log in to reply
Good point! I edited the question to include A B < C D and A D < B C .
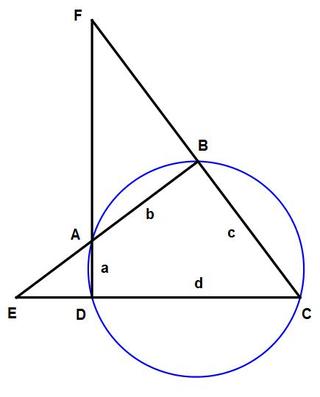
Let ( D A , A B , B C , C D ) = ( a , b , c , d ) . Then
A F = b d 2 − b 2 a b + c d
B F = b d 2 − b 2 c b + a d
A E = a c 2 − a 2 d a + b c
D E = a c 2 − a 2 b a + d c
We have
b
=
7
a
A
F
=
b
D
E
b
+
A
F
+
B
F
=
2
8
a
+
A
E
+
D
E
=
1
2
Solve for a , b , c , d to get
( a , b , c , d ) = ( 3 , 7 , 9 , 1 1 )
Letting s = 2 1 ( a + b + c + d ) , we find the area
A = ( s − a ) ( s − b ) ( s − c ) ( s − d ) = 4 8
Use chord theorem and similarity of two triangles to solve for remaining two sides of quadrilateral. The side d=7(12/28)=3, as two triangles are similar.
The first integer area solution for quadrilateral was for sides 7,9,11,3.
There are general solutions, 7, b>0, (2/3)b+5 and 3. The solution for all integer sides including two triangles is for b=27, but area is ~114.2.
Answer=48
Since it is given that ∠ E = ∠ F , and ∠ D A E = ∠ B A F by vertical angles, △ A B F ∼ △ A D E by AA similarity.
Since ∠ A D C + ∠ A B C = 1 8 0 ° as opposite angles in an inscribed quadrilateral and ∠ A B F + ∠ A B C = 1 8 0 ° as a straight line, ∠ A D C = ∠ A B F , and since ∠ F = ∠ F by the reflexive property, △ A B F ∼ △ C D F by AA similarity. Likewise, △ A E D ∼ △ C B E . Therefore, all four triangles △ A B F , △ A D E , △ C D F , and △ C B E are similar to each other.
Since ∠ A B F + ∠ A B C = 1 8 0 ° from a straight line and ∠ A B F = ∠ A B C from similar triangles, ∠ A B F = ∠ A B C = 9 0 ° . By a similar argument, ∠ C D F = ∠ A D E = 9 0 ° .
Since the ratio of the perimeters equal the ratio of the sides in similar triangles, P △ A B F P △ A D E = A B A D , or 2 8 1 2 = 7 A D , which solves to A D = 3 .
By Pythagorean's Theorem on △ A D E , 3 2 + D E 2 = A E 2 , and by the perimeter of △ A D E , 3 + D E + A E = 1 2 , and these two equations solve to D E = 4 and A E = 5 . The area of △ A D E is then A △ A D E = 2 1 ⋅ A D ⋅ D E = 2 1 ⋅ 3 ⋅ 4 = 6 .
The scale factor k of similar triangles △ C B E to △ A D E is k = D E B E = 4 5 + 7 = 3 , so the area of △ C B E is A △ C B E = k 2 ⋅ A △ A D E = 3 2 ⋅ 6 = 5 4 .
Therefore, the area of quadrilateral A B C D is A A B C D = A △ C B E − A △ A D E = 5 4 − 6 = 4 8 .