A difficult 2018 problem

Let $f(x) = ax^3+bx^2+cx+d$ . Then we have:

$\begin{cases} x=1: & a+b+c+d = 2 & ...(1) \\ x=2: & 8a+4b+2c+d = 0 & ...(2) \\ x=3: & 27a+9b+3c+d = 1 & ...(3) \\ x=4: & 64a+16b+4c+d = 8 & ...(4) \end{cases}$

$\begin{cases} (2)-(1): & 7a+3b+c = -2 & ...(5) \\ (3)-(2): & 19a+5b+c = 1 & ...(6) \\ (4)-(3): & 37a+7b+c = 7 & ...(7) \end{cases}$

$\begin{cases} (6)-(5): & 12a+2b = 3 & ...(8) \\ (7)-(6): & 18a+2b = 6 & ...(9) \end{cases}$

$\begin{array} {rll} (9)-(8): & 6a = 3 & \implies a = \frac 12 \\ (8): & 6+2b = 3 & \implies b = - \frac 32 \\ (5): & \frac 72-\frac 92 + c = -2 & \implies c = - 1 \\ (1): & \frac 12 - \frac 32-1 + d = 2 & \implies d = 4 \end{array}$

Therefore, $f(x) = \frac 12 x^3 - \frac 32 x^2 - x + 4$ and $f(2018) = \boxed{4102864416}$ .

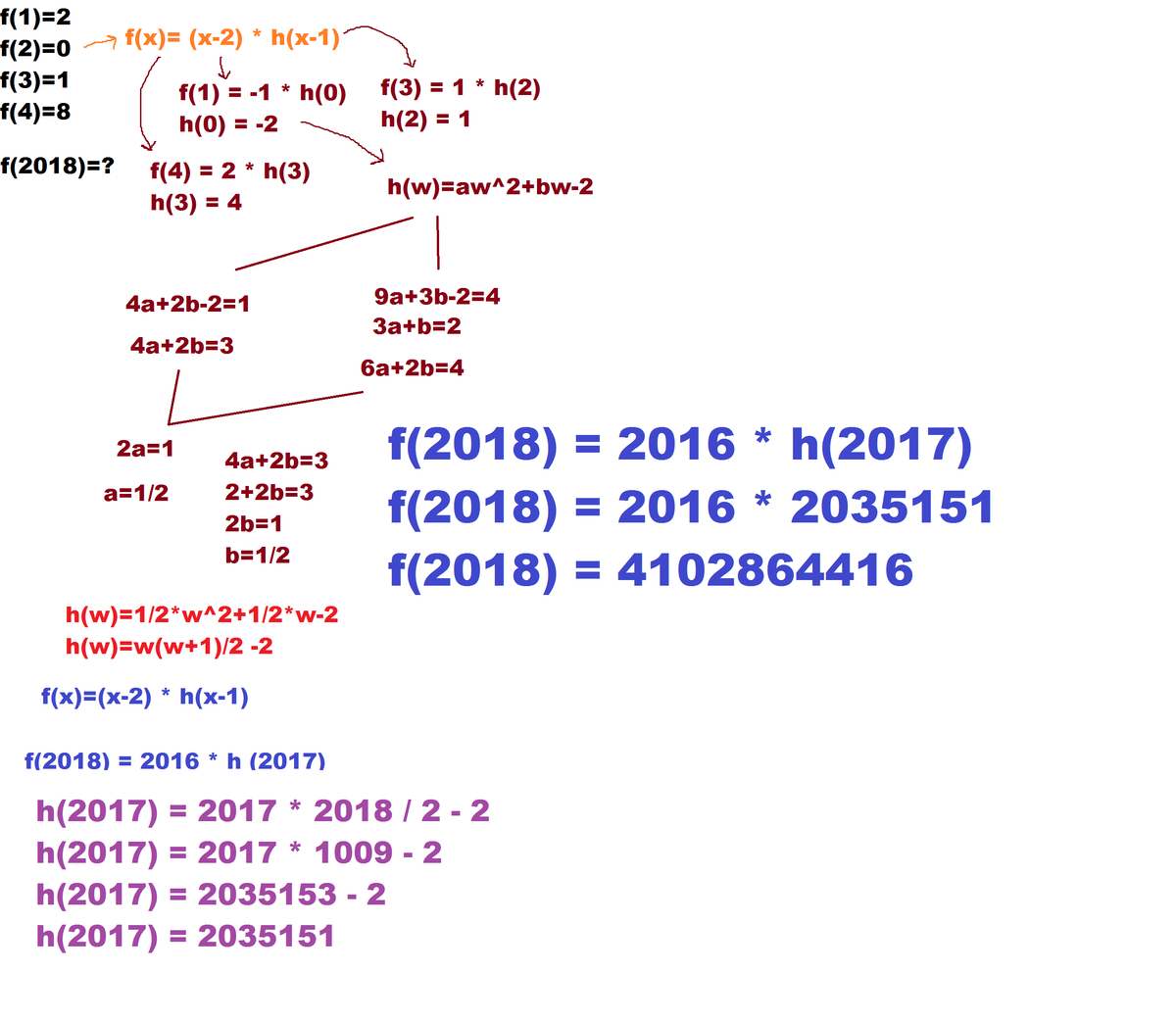
Orange:

Factor Theorem. If $f(a)=0$ , then $f(x)$ has a factor of $x-a$ [I used $h(x-1)$ instead of $h(x)$ to get $h(0)$ in one of the new equations later on]

$h(w)$ is a quadratic since a cubic [like $f(x)$ ] divided by a linear [like $x-2$ ] gives a quadratic. [Also, I called the input w in the image in order not to make it seem confusing that the relation uses x-1]

Maroon:

Substitute 1, 3, and 4 for x in $f(x)=(x-2) \times h(x-1)$ to get more information about h [Since $f(x)$ and $x-2$ will equal 0 when $x=2$ , we do not substitute it, since this will just give $0=0$ and will not give any new information]. Then, because $h(0)=-2$ , we know that $h(w)=aw^2+bw-2$ for some constants $a$ and $b$ .

Substitute 2 and 3 for w in $h(w)=aw^2+bw-2$ to get a system of linear equations in terms of $a$ and $b$ . Using the system, solve for $a$ and $b$ . We find that they both equal one-half.

Red:

Substitute the values of $a$ and $b$ in $h(w)=aw^2+bw-2$ to get the rule for h. Also, rearrange the right-hand side in order to make the rule easier to use later on. The final result is $h(w)=\frac{w(w+1)}{2}-2$

First Blue:

Substitute $x=2018$ in $f(x)=(x-2) \times h(x-1)$ , thus getting $f(2018)=2016 \times h(2017)$

Purple:

Substitute $w=2017$ in $h(w)=\frac{w(w+1)}{2}-2$ to get $h(2017)$

Second [and bigger] Blue:

Substitute the value of $h(2017)$ in $f(2018)=2016 \times h(2017)$ to get the final answer.

By Lagrange Interpolation, $f(x) \; = \; \frac{2}{-6}(x-2)(x-3)(x-4) + \frac{1}{-2}(x-1)(x-2)(x-4) + \frac{8}{6}(x-1)(x-2)(x-3) \; = \; \tfrac12x^3 - \tfrac32x^2 - x + 4$ and so $f(2018) = \boxed{4102864416}$ .

A cubic polynomial is in the form of $f(x) = ax^3 + bx^2 + cx + d$ .

For $f(1) = 2$ , we have $a \cdot 1^3 + b \cdot 1^2 + c \cdot 1 + d = 2$ or $a + b + c + d = 2$ .

For $f(2) = 0$ , we have $a \cdot 2^3 + b \cdot 2^2 + c \cdot 2 + d = 0$ or $8a + 4b + 2c + d = 0$ .

For $f(3) = 1$ , we have $a \cdot 3^3 + b \cdot 3^2 + c \cdot 3 + d = 1$ or $27a + 9b + 3c + d = 1$ .

For $f(4) = 8$ , we have $a \cdot 4^3 + b \cdot 4^2 + c \cdot 4 + d = 8$ or $64a + 16b + 4c + d = 8$ .

Solving the system of equations $a + b + c + d = 2$ , $8a + 4b + 2c + d = 0$ , $27a + 9b + 3c + d = 1$ , and $64a + 16b + 4c + d = 8$ gives $a = \frac{1}{2}$ , $b = -\frac{3}{2}$ , $c = -1$ , and $d = 4$ , so the cubic polynomial is $f(x) = \frac{1}{2}x^3 - \frac{3}{2}x^2 - x + 4$ .

Therefore, $f(2018) = \frac{1}{2}(2018)^3 - \frac{3}{2}(2018)^2 - (2018) + 4 = \boxed{4102864416}$ .