A Difficult Integral
∫ 0 ∞ e 2 x − 1 x 4 d x = b a e
The equation above holds true for coprime positive integers a and b , and e denotes the Euler's number .
What is the value of a + b ?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The given integral can be written as
e ∫ 0 ∞ x 4 e − 2 x d x
Substituting 2 x = t
we have
3 2 e ∫ 0 ∞ t 4 e − t d t
So we have,
3 2 e Γ ( 5 )
= 3 2 2 4 e
= 4 3 e
Integrating by parts the function x 4 e 1 − 2 x within the given limits, we get the value of the integral as 4 3 e , making a = 3 , b = 4 , a + b = 7 .
This is no solution...you just wrote the answer.....in a horribly pixelated picture. If you want to post a picture...I suggest you use daum equation editor and write out a full solution and not just the answer.
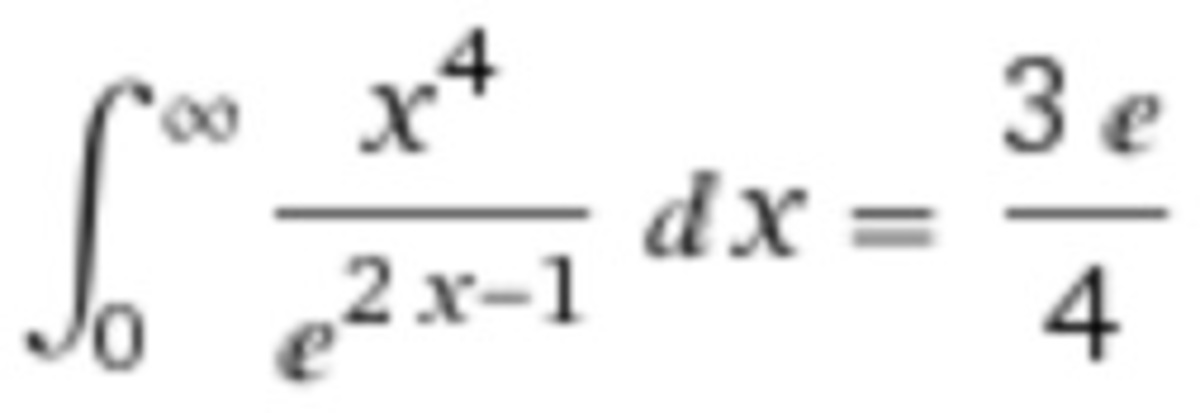
∫ 0 ∞ e 2 x − 1 x 4 = e ∫ 0 ∞ x 4 e − 2 x d x = e ∫ 0 ∞ ∂ k 4 ∂ 4 e − k x d x = e ∂ k 4 ∂ 4 ∫ 0 ∞ e − k x d x = e ∂ k 4 ∂ 4 ( k 1 ) = k 5 4 ! e = 3 2 2 4 e = 4 3 e Let k = 2
Therefore a + b = 3 + 4 = 7 .