A direct shot in the far right corner
In a simulation of a pool game, the pool table is a rectangle with a horizontal width of 15 units and a vertical length of 30 units.
The left bottom corner of this rectangle is at the origin of an reference frame with standard orientation. You have two billiard balls of radius 1 unit, the first is the cue ball (drawn in light green) and is placed at , the second is the target ball and is placed at . You want to shoot the cue ball (green) in a certain direction, such that it collides with the target ball, causing it to move to the target point which, in this problem, is the far right corner, whose coordinates are . Find the angle that the direction of your shot of the cue ball makes with the positive -axis, in radians , and report .
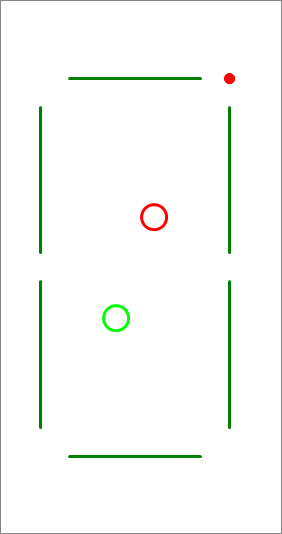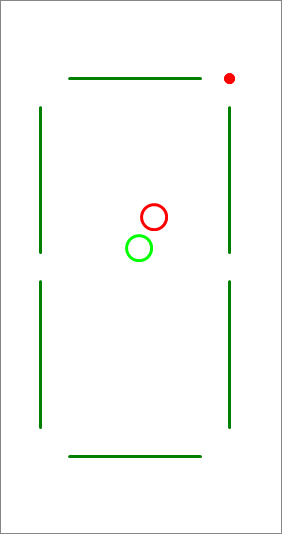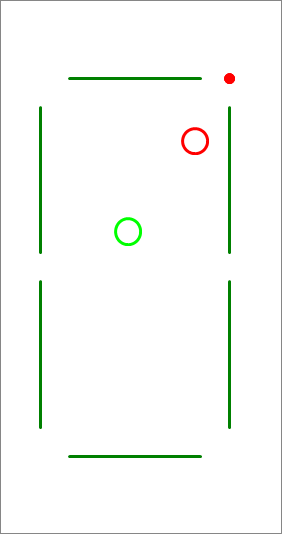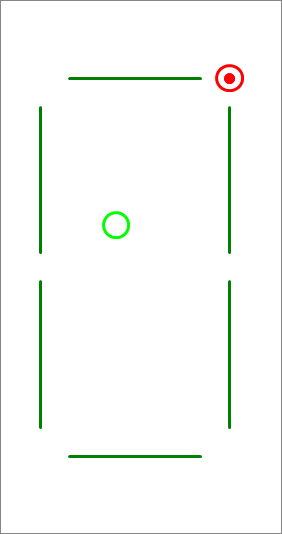
The answer is 1254.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.