A probability problem by Anish Roy
Let be a positive intger satisfying the following property: If dominoes are placed on a chessboard with each domino covering exactly two unit squares, then one can always place one more domino on the board without moving any other dominoes. Determine the maximum value of
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The maximum value of n is 1 1 . The fig. below shows an arrangement of 1 2 dominoes in which one cannot place any more dominoes on the board. Consequently n ≤ 1 1 .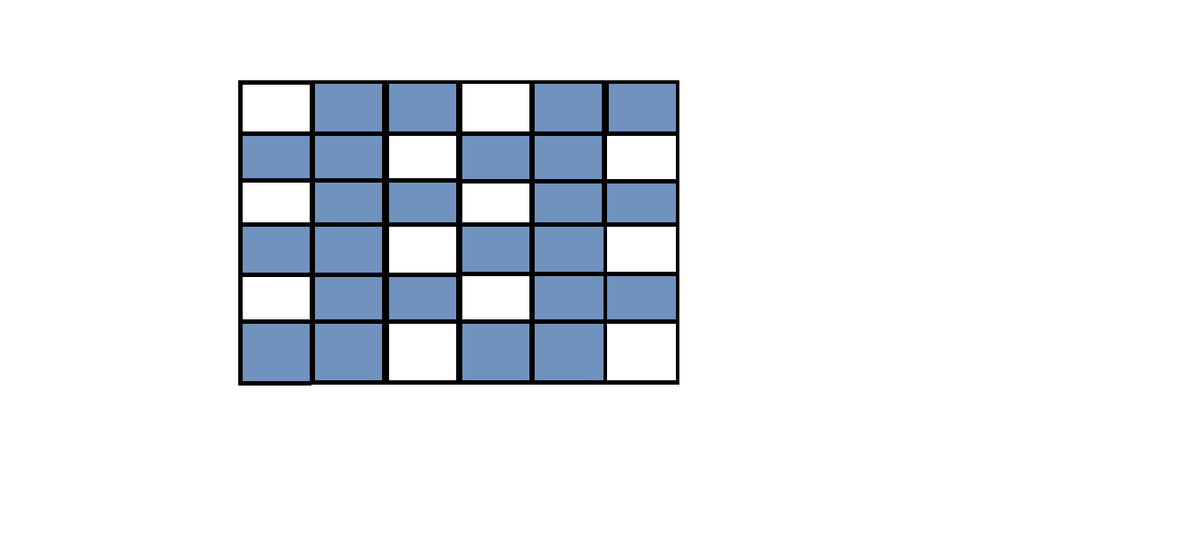 It suffices to show that one can always place one more domino if there are
1
1
dominoes on the board. We approach the problem indirectly by assuming that there is an arrangement of
1
1
dominoes such that one cannot place anothetr domino on the board. Hence there are
3
6
−
2
2
=
1
4
unit squares not covered by the dominoes. Let
S
1
denote the upper
5
×
6
sub board of the given chessboard. Because we cannot place one more domino on the board, at least one of any two neighbouring unit squares (unit squares sharing an edge) is covered by a domino. Hence there are at least
3
unit squares in
S
2
that are covered by dominoes, so there are at most three uncovered unit squares in
S
2
. Thus there are at least
1
non-covered unit squares in
S
1
that is,
∣
A
∣
≥
1
1
. Let
S
3
dente the lower
5
×
6
sub-board of the given chessboard. Let
B
denote the set of dominoes that lie (completely) in
S
3
. We will define a map
f
from
A
to
B
. By the definition of
S
1
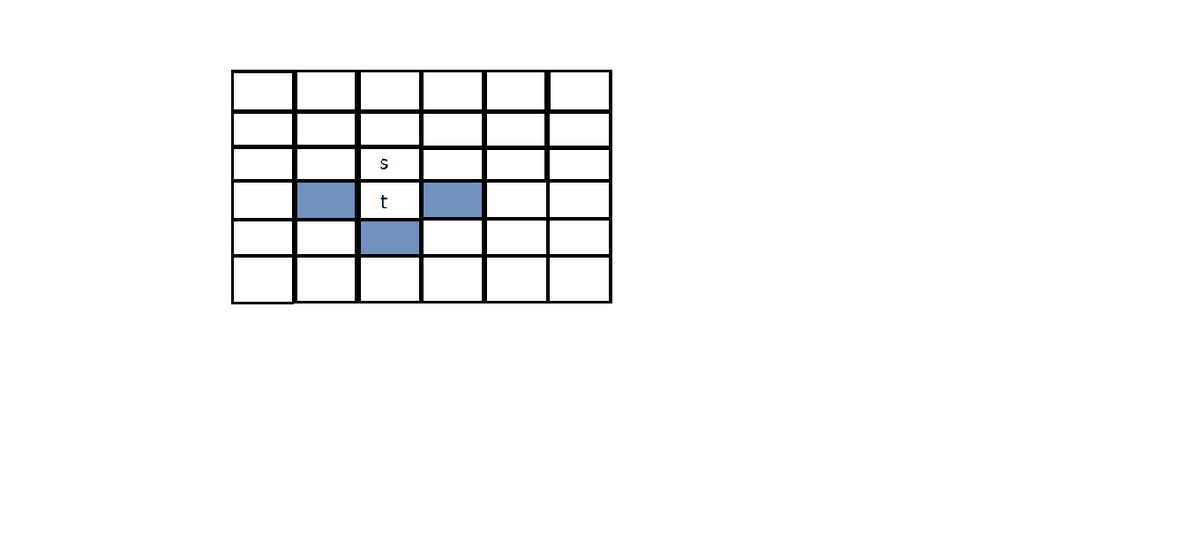
, there is always a unit square
t
directly below a unit square
s
S
1
. Further assume that
s
is in
A
. Then
t
must be covered by a domino
d
in
S
3
, because otherwise we could place one more domino covering
s
and
t
. We define
f
(
s
)
=
t
. We claim that
f
is injective. If not, then there are
s
1
and
s
2
in
A
with
f
(
s
1
)
=
f
(
s
2
)
=
t
. This means that
t
covers the unit squares directly below
s
1
and
s
2
. Hence
s
1
and
s
2
must be neighbours.
It suffices to show that one can always place one more domino if there are
1
1
dominoes on the board. We approach the problem indirectly by assuming that there is an arrangement of
1
1
dominoes such that one cannot place anothetr domino on the board. Hence there are
3
6
−
2
2
=
1
4
unit squares not covered by the dominoes. Let
S
1
denote the upper
5
×
6
sub board of the given chessboard. Because we cannot place one more domino on the board, at least one of any two neighbouring unit squares (unit squares sharing an edge) is covered by a domino. Hence there are at least
3
unit squares in
S
2
that are covered by dominoes, so there are at most three uncovered unit squares in
S
2
. Thus there are at least
1
non-covered unit squares in
S
1
that is,
∣
A
∣
≥
1
1
. Let
S
3
dente the lower
5
×
6
sub-board of the given chessboard. Let
B
denote the set of dominoes that lie (completely) in
S
3
. We will define a map
f
from
A
to
B
. By the definition of
S
1
, there is always a unit square
t
directly below a unit square
s
S
1
. Further assume that
s
is in
A
. Then
t
must be covered by a domino
d
in
S
3
, because otherwise we could place one more domino covering
s
and
t
. We define
f
(
s
)
=
t
. We claim that
f
is injective. If not, then there are
s
1
and
s
2
in
A
with
f
(
s
1
)
=
f
(
s
2
)
=
t
. This means that
t
covers the unit squares directly below
s
1
and
s
2
. Hence
s
1
and
s
2
must be neighbours.
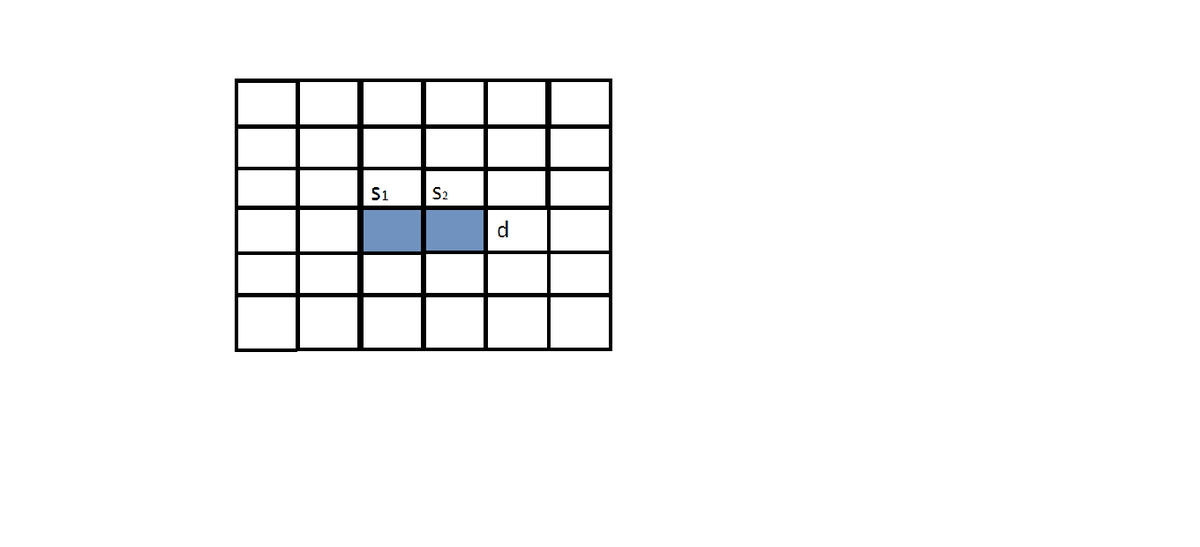 But then we can place an extra domino on
s
1
and
s
2
, which is a contradiction. Thus
f
is indeed injective, and
∣
A
∣
≤
∣
B
∣
. It follows that
∣
B
∣
≥
1
1
. But there are only
1
1
dominoes. Hence
∣
B
∣
=
1
1
. This means that all
1
1
dominoes lie completely in
S
3
; that is , the top row is not covered by any dominoes at all. But we can certainly put three more dominoes there, which contradicts the maximality of this arrangement. Hence our assumption was wrong, and one can always place one more domino on a
6
×
6
chessboard that is covered by
1
1
dominoes.
But then we can place an extra domino on
s
1
and
s
2
, which is a contradiction. Thus
f
is indeed injective, and
∣
A
∣
≤
∣
B
∣
. It follows that
∣
B
∣
≥
1
1
. But there are only
1
1
dominoes. Hence
∣
B
∣
=
1
1
. This means that all
1
1
dominoes lie completely in
S
3
; that is , the top row is not covered by any dominoes at all. But we can certainly put three more dominoes there, which contradicts the maximality of this arrangement. Hence our assumption was wrong, and one can always place one more domino on a
6
×
6
chessboard that is covered by
1
1
dominoes.