The Perfect Tetris?
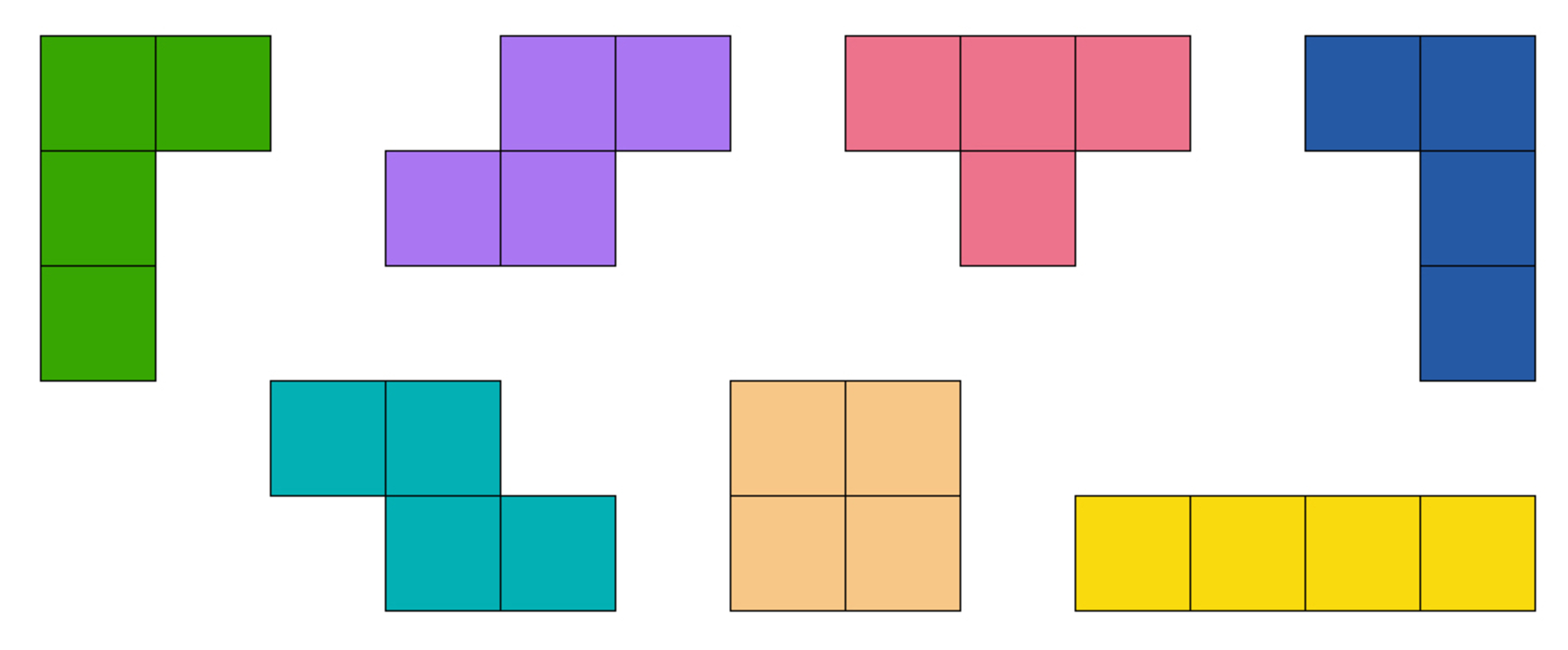
I received a set of 21 tetraminos, consisting of 3 copies each of the 7 distinct pieces.
I want to arrange them into a nice rectangle, of area . For how many rectangle shapes can I fit all of them nicely?
Note : It doesn't matter if there are 2 ways to fill in the rectangle. Rotations / Reflections / Orientation of the rectangle also doesn't matter.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can mark all the squares of any lattice rectangle either white or black as we would with a 8 × 8 chessboard. Any so-marked lattice rectangle that has at least one even side will have an equal number of squares marked white and marked black.
The area of any lattice rectangle that can be formed by 3 sets of 7 pieces of 4 squares each is 8 4 , as already noted. We can see that there are only 5 possible candidates, which are lattice rectangles of sides as follows:
2 × 4 2
3 × 2 8
4 × 2 1
6 × 1 4
7 × 1 2
Hence, in all possible cases, the number squares marked black and white are equal. By laying any of the 7 of the tetramino pieces on a marked lattice rectangle, we can readily see that for all the pieces but one, each of the pieces will have 2 white squares and 2 black squares. The odd piece is the T piece, which will have either 1 white square and 3 black squares or vice-versa. Combining 3 such T pieces will always result in an unequal number of white and black squares. Ergo, the 2 1 tetramino pieces cannot successfully tile any of the possible lattice rectangle candidates, and so the answer is 0 .