Tiling With Squares
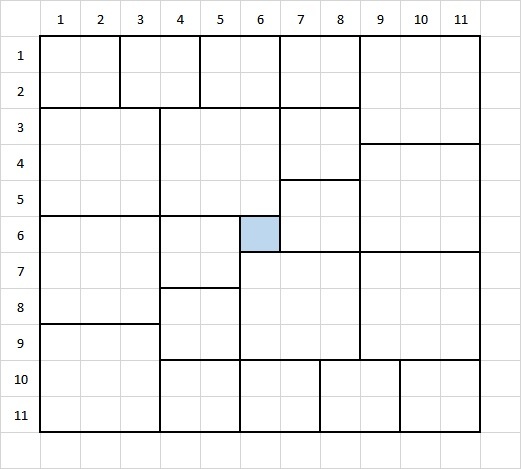
A floor with dimensions 1 1 × 1 1 will be covered by some tiles with dimensions 1 × 1 , 2 × 2 , or 3 × 3 without overlapping. Find the least possible number of 1 × 1 tiles that will be needed.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
You have only shown that "1" is possible. How do you know that "0 1x1 tile" is impossible?
Do you know how to explain that 1 is indeed the minimium?
How did you figure out this tiling?
@gavin how do you fill 11 spaces with 2x2 tiles with no remainder?
0 is possible, tile 2x2s along the top and left, leaving a 9x9 space unfilled, then use 3x3 to easily fill the remaining space
From RJ's configuration, we see that we can use just a single 1 × 1 tile. It remains to show that we cannot use 0 1 × 1 tiles. We will prove this by contradiction.
Suppose there exist a tiling with only
2
×
2
and
3
×
3
tiles.
Color each alternating row blue and then green.
Then, each
2
×
2
tile covers 2 blue and 2 green tiles, and each
3
×
3
tile either covers 6 blue and 3 green, or 3 blue and 6 green tiles. Let the number of such tiles be
A
,
B
and
C
respectively.
Since there are 6 × 1 1 = 6 6 blue tiles and 5 × 1 1 = 5 5 green tiles, hence we get the system of equations
2 A + 6 B + 3 C = 6 6 2 A + 3 B + 6 C = 5 5
Taking the difference of the two equations, we get that 3 ( B − C ) = 1 1 ⇒ B − C = 3 1 1 . This is not possible since B and C are integers, hence we have a contradiction.
Follow up questions: This solution shows that if 6 ∣ n , then we will need at least 1 tile. Can we figure out the answer for general n ? I suggest looking at cases based on n ( m o d 6 ) .
- The cases of 6 n + 2 , 6 n + 3 , 6 n + 4 are easy to deal with
- What about 6 n + 5 which is like this? Is 1 tile enough? Can we use the 1 1 × 1 1 example in our construction?
- What about 6 n + 1 ? Is 1 tile enough?
wrong the answer is 2
Log in to reply
Given that there is a configuration which uses only a single 1 × 1 square (IE Rj's solution), the minimum number needed is at most 1.