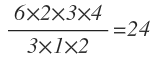A Distorted Grid
 In this grid, each rectangle is labelled with its area. What area should replace the question mark?
In this grid, each rectangle is labelled with its area. What area should replace the question mark?
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
22 solutions
This is the most brilliant method, according to me! :) But I feel that you could've elaborated in the beginning, as where 3 and 1 came from. Of course, one look at the diagram tells us what's needed, but that's to those who have followed..
Don't get it. It is not all clear to me why I have to bother with the height of R3 and width of C3. Or why I divide by 2 (and how do I know that it's division?). Completely opaque to me, esp. after step 2
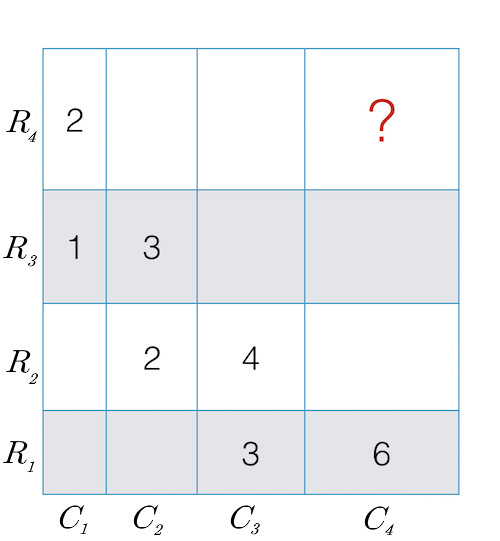
Denote the columns of the grid from left to right C 1 , … , C 4 and the rows of the grid from down to up R 1 , … , R 4 .
Consider the rectangles in positions ( C 2 , R 2 ) and ( C 3 , R 2 ) . Since their heights are the same, we conclude C 3 = 2 C 2 , therefore the rectangle in position ( C 3 , R 3 ) has area 3 × 2 = 6 .
Similarly, we find that 2 C 3 = C 4 so the rectangle in position ( C 4 , R 3 ) has area 6 × 2 = 1 2 . Also we find that 2 R 3 = R 4 , so the area of the rectangle in position ( C 4 , R 4 ) is 1 2 × 2 = 2 4 .
Why make it more complicated than is necessary? Just recognise the relationship between rows and use that to calculate the required area
Log in to reply
It's just a way of visualising what I did in my head. If I just said the rectangle next to the 3 is 6, people may not understand what I'm doing.
just measure it - its not 24 . and the other areas are not valid either. regardless of what rectangle you choose to be the point of origin of these X numbered-arbitrary measurements . Dumb question
Log in to reply
In geometry, you're not allowed to base answers off of the picture. Of course you have to get your information from it, but size and scale aren't accurate. The picture is simply there to give you an idea of what you're doing.
Ever heard of "NOT DRAWN TO SCALE"? Dumb person
Too good innovative question
Though dictation of the grids are little complicated to make out, I thank a lot.
RE: Since their heights are the same, we conclude C3 = 2C3 , therefore the rectangle in position (C3 R3) has area 3 x 2 = 6.
This seems like a huge leap to me from the "since" to the "therefore"--missing several steps to make this clear.
Let the partitioned rectangle of area 1 have a width of x units and a height of y units. Then x y = 1 .
Then since the top left area 2 rectangle has the same width as the area 1 rectangle, its height must be 2 y . This will also be the height of the rectangle marked "?".
Next, since the area 3 rectangle has the same height as the area 1 rectangle, its width must be 3 x . The area 2 rectangle below the area 3 rectangle then also has width 3 x , and so the area 4 rectangle must have width 6 x . The area 3 rectangle below the area 4 rectangle must then also have width 6 x , and so the area 6 rectangle has width 1 2 x . The "?" rectangle must then also have width 1 2 x .
The "?" rectangle thus has height 2 y , width 1 2 x , and area 1 2 x ∗ 2 y = 2 4 ∗ x y = 2 4 ∗ 1 = 2 4 .
(Note that the height of the whole rectangle is 2 y + y + 3 2 y + ( 4 3 ) ( 3 2 ) y = 6 2 5 y , and has an overall width of x + 3 x + 6 x + 1 2 x = 2 2 x . Its area is thus 2 2 x ∗ 6 2 5 y = 3 2 7 5 x y = 9 1 . 6 6 6 . . . . )
Beautiful solution
clumsy answer
this is the most intelligible of the 3 so far.
The answer and the question provider may be the same person ... but whoever it is couldn't explain it properly ... include some basics and rules as well applied to your approach ...
the factors of columns can be used
1 X 3 = 3 increased by 3 factors
2 X 2= 4 increased by 2 factors
3 X 2 = 6 increased by 2 factors
then
2 X 3 X 2 X 2 = 24
did the same - we have factors for pairs of columns and this covers all 4 columns so this was the simplest way to calculate.
Very simple solution:
Each adjacent rectangle has one side in common with the other. Starting from the top left-most corner and proceeding downwards and towards right, we can write the area of each rectangle as:
a*b = 2
b*c = 1
c*d =3
d*e = 2
e*f = 4
f*g = 3
g*h = 6
The missing block, with area a*h = 24
Last step is to multiply and divide all the equations mentioned above, such that you get. (a b)/(b c)=2 -->a c=2 Then you can similarly combine the rest of the equations till you find a h=24
right...i did the same way...
When we go across one column at a time, starting at two, we can take rectangles in the same row as each other to see how much wider the column to the right is than the one to the left. 3 is 3 times wider than 1, so we multiply the top left corner by 3 to get 6; 4 is 2 times wider than 2, so we multiply by 2 to get 12; 6 is 2 times wider than 3, so we multiply 12 by 2 to get 24, the top right corner.
Using the given areas of some squares, we can fill in the blanks from their relative proportions. Thus:
 From these squares, we can see that the top line goes from 2 to 6, or 3x, then 6 goes to 12, and, since 3 goes to 6 on the bottom right corner, we know that in the top right corner, 12 goes to 24, giving us our answer.
☺☺☺☺
From these squares, we can see that the top line goes from 2 to 6, or 3x, then 6 goes to 12, and, since 3 goes to 6 on the bottom right corner, we know that in the top right corner, 12 goes to 24, giving us our answer.
☺☺☺☺
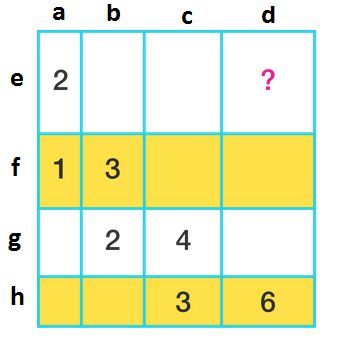 Let's name the horizontal sides
a, b, c
and
d
and the vertical ones
e, f, g
and
h
. We have the following 7 equations (horizontal size x vertical size = rectangle area):
ae = 2, af = 1, bf = 3, bg = 2, cg = 4, ch = 3, dh = 6
. We need to find the area
de
.
We start from the last equation:
d = 6/h
. We substitute
h
with it value from the previous equation and so on, going backwards. We get: d = 6/h = 6/(3/c) = 2c = 8/g = 8/(2/b) = 4b = 12/f = 12/(1/a) = 12a = 24/e. Hence de =
24
.
Let's name the horizontal sides
a, b, c
and
d
and the vertical ones
e, f, g
and
h
. We have the following 7 equations (horizontal size x vertical size = rectangle area):
ae = 2, af = 1, bf = 3, bg = 2, cg = 4, ch = 3, dh = 6
. We need to find the area
de
.
We start from the last equation:
d = 6/h
. We substitute
h
with it value from the previous equation and so on, going backwards. We get: d = 6/h = 6/(3/c) = 2c = 8/g = 8/(2/b) = 4b = 12/f = 12/(1/a) = 12a = 24/e. Hence de =
24
.
Ler a = the horizontal length of the upper left corner. Since the area = 2, the vertical length must be 2/a. This is enough information to work our way around the rectangle. We find the vertical lengths going down to be: 2/a,1/a, 2/3a,and 1/2a. The horizontal lengths from left to right are: a,3a, 6a, and 12a. We can use any known rectangle to deduce that a = 1. The dimensions of the ? square are 2/a x 12a. letting a =1, we get 24. Ed Gray
The easiest way is to compare the width of the columns to each other, as each columns fits a whole number of times into the one next to it.
The 2nd column is exactly 3x as wide as the 1st, due to the "1" and "3" rectangles in the second row having the same height, which means the difference in area must come from the width
Similarly, the "2" and "4" rectangles in the 3rd row show us [by virtue of being in the same row] that the 3rd column must be twice the width of the 2nd.
Finally, the "6" rectangle is obviously two of the "3" rectangle right next to it side by side, which must mean that the entirety of the last column is 2x the width of the 3rd column.
Thus, the right-most column is 3 x 2 x 2 = 12 times as wide as the left-most one, which means that the rectangle whose area we are being asked must have an area that's 12x the size of the left-most rectangle in that same row, of which we know the area. So that's 12 x 2 = 2 4
From the second row, we know that the second column has three times the area as the first column. From the third row, the third column has twice the area of the second column and from the fourth row, the fourth column has twice the area as the third column. Therefore the square in question is 2 * 3 * 2 * 2 = 24.
One way of solving it is by observing the relationship between numbers as they go up the rows on the grid.
Moving from 4th to 3rd: a 3 changes into a 4 (×4/3) Moving from 3rd to 2nd: a 2 changes into a 3 (×3/2) Moving from 2nd to 1st: a 1 changes into a 2 (×2)
Since the numbers are on the same grid, all the numbers must follow this multiplier rule when moving up the rows (they get divided instead when moving down).
Then, the 6 on the 4th row must be multiplied by 4/3, then 3/2 and lastly by 2 to get to the 1st row.
6 x 4/3 × 3/2 × 2 = 24!
Of course this also works by examining the columns instead as you go from left to right. Try it! :D
With the same line of reasoning, you'll end up with:
2 × 3 x 2 x 2 = 24!

Denote the rows of the grid from down to up R1, R2, R3 and R4 and the columns of the grid from left to right C1, C2, C3 and C4.
- Let the width of (R1, C3) be w... [1]
-
Let the height of (R2, C2) be h... [2]
-
Width of (R2, C3) = Width of (R1, C3) = w
-
Height of (R2, C3) = Height of (R2, C2) = h
-
Area of (R2, C3) = Width of (R2, C3) * Height of (R2, C3)
- w*h = 4... [3]
(R1, C4) has the same height as (R1, C3), but twice the area. Therefore, from [1] , the width of (R1, C4) = 2*w... [4]
(R3, C2) has the same width as (R2, C2), but 1.5 times the area. Therefore, from [2] , the height of (R3, C2) = 1.5*h... [5]
Height of (R3, C1) is the same as (R3, C2). Therefore, from [5] , the height of (R3, C1) = 1.5*h... [6]
(R4, C1) has the same width as (R3, C1), but twice the area. Therefore, from [6] , the height of (R4, C1) = twice the height of (R3, C1) = 2 (1.5 h) = 3*h... [7]
- Width of (R4, C4) = Width of (R1, C4) = 2*w (From [4])
- Height of (R4, C4) = Height of (R4, C1) = 3*h (From [7])
- Area of (R4, C4) = Width of (R4, C4) * Height of (R4, C4) = (2 w) (3 h) = 6 w*h
But w h = 4 (From [3]) Therefore, Area of (R4, C4) = 6 (w h) = 6 (4) = 24
You don't have to work out the height and width of the rectangles.
Those on the same row have the same height. So those in column three are twice as wide as those in column two. And those in column four are twice as wide as those in column three.
Sim: row three are 1.5 times as high as row two.
Above the 4 is a 6, then a 12. To the right of the 12 is a 24
Simply ? = 2 * 3/2 * 4/3 * 6
(From the relationship between the rows from the given areas)
Areas for marked rectangles are:
ab=2; ac=1; cd=3; de=2; ef=4; fg=3; gh=6
and for the unknown area rectangles bh=Area of Unknown
eleminating all variables except "b"
a= b 2 ; c= 2 b ; d= b 6 ; e= 3 b ; f= b 1 2 ; g= 4 b ; h= b 2 4
Now substituting on last equation for unknown area b* b 2 4 =Area of Unknown Area of Unknown=24
Take any four rectangles such that all rectangles occupy only two rows and two columns. We'll choose the middle 4 rectangles for this example. Since the area of a rectangle is base * height, we can see that if we multiple the top left rectangle's area with the area of the bottom right rectangle, we obtain an area equal to the top right rectangle's area times the bottom left rectangle's area.
a b
c ||A1||A2||
d ||A3||A4||
A1 = a * c, A2 = b * d, A3 = a * d, A4 = b * d
A1
A4 = A2
A3 = a * b * c * d
Namely, 3 * 4 = 2 * x where x is the area of rectangle above the rectangle with area 4. We get that x = 6. We can use this algorithm to solve for the area in the bottom right corner. We get that the area is .5 Now let A1 be the area of the top left rectangle, A2 be the area of the top right rectangle, A3 be the area of the bottom left rectangle, and A4 be the area of the bottom right rectangle. ||A1|| || ||A2|| || || || || || || || || || || ||A3|| || ||A4||
Now A1A4 = A2A3 2*6 = ? * .5 ? = 24
My Solution is probably less elegant than most. I walked the given areas to calculate the sides.
Given R3,C1 has area 1, both sides must be 1. Therefore, the height of R4,C1 is 2. That gives us the height of R4,C4.
Now, the width of R2,C3 has to be 3. since we know the height is 1.
Given a width of 3 and area of 2 for R2,C2, the height has to be 2/3
Given a height of 2/3 and an area of 4, the width of R2,C3 is 6
Given a width of 6 and an area of 2, the height of R1C3 is 1/2
Given a height of 1/2 and an area of 6, the width of R1,C4 is 12 which is also the width of R4,C4
2x12 = 24
This could be a bit of a crude explanation but here goes...
So there were two ways I saw to do this using proportions only. I personally used the vertical way and so will explain that method. Because the ? is in the same column as the 6, we did not need to account for any horizontal change from there. Now if we assume the top row is R1 and continue down to the bottom at R4, we see that going from R1 to R2 means the area will half. From R2 to R3, it dropped a third. R3 to R4 dropped a quarter of the area.
Now to reverse that starting from 6:
6* 4/3 = 8
8* 3/2 = 12
12 * 2/1 = 24
And so area of ? is 24.
It may be a crude way, but works for these kind of problems.
First assume the rectangle whose area is 4 as a square. This means that it's each side is 2. Solve for breadths of adjacent rectangles and at last we get 6 as length and 4 as breadth for required rectangle. So, the area becomes 24.

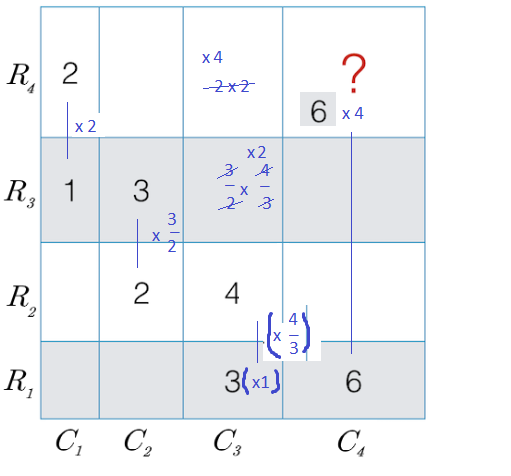
One way to solve this question is to find the common sides with another rectangles. For our rectangle, the rectangles with area 2 & 6 share a common height and width respectively.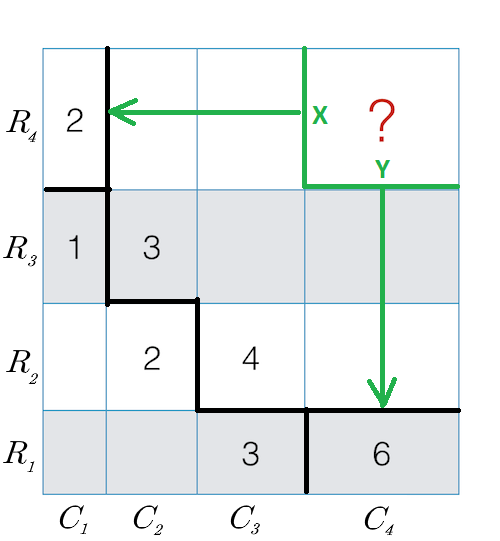
So our answer will include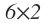 But wait, multiplying 6 and 2 will also include height of R1 and width of C1. So divide the expression with their height and width, which can be done by putting 3 & 1 in the denominator i.e
But wait, multiplying 6 and 2 will also include height of R1 and width of C1. So divide the expression with their height and width, which can be done by putting 3 & 1 in the denominator i.e
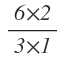 Now, our expression still contains height of R3 and width of C3 in the denominator, So multiply the expression with 3 & 4.
Now, our expression still contains height of R3 and width of C3 in the denominator, So multiply the expression with 3 & 4.
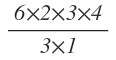 . And finally notice that the expression still contains height of R2 and width of C2 in the numerator. So divide the expression by 2.
. And finally notice that the expression still contains height of R2 and width of C2 in the numerator. So divide the expression by 2.