A Divisibility Addition

Number Theory Level 1

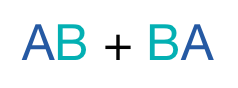
If we take a certain 2-digit integer and reverse its digits to form another 2-digit integer, then the sum of these two numbers is always divisible by which of the following numbers?

9 10 11 12

View wiki
Chung Kevin by Chung Kevin , 45, Australia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Let the two digit number be A B ‾ = 10 A + B \overline{AB}=10A+B .Then the number forned by reversing its digits will be B A ‾ = 10 B + A \overline{BA}=10B+A .Their sum would be: A B ‾ + B A ‾ = ( 10 A + B ) + ( 10 B + A ) = 11 A + 11 B = 11 ( A + B ) \begin{aligned} \overline{AB}+\overline{BA}&=(10A+B)+(10B+A)\\ &=11A+11B=11(A+B)\end{aligned} Therefore the sum of a two digit number and the number formed by reversing its digits is always divisible by 11 \boxed{11}

12 Helpful 0 Interesting 0 Brilliant 0 Confused

Is there a name for this theorem or for this math fact?

Bryan Gonzalez - 5 years, 1 month ago

Log in to reply

I don't think so

Mohamed Refaee - 5 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...