A geometry problem by Ricky Huang
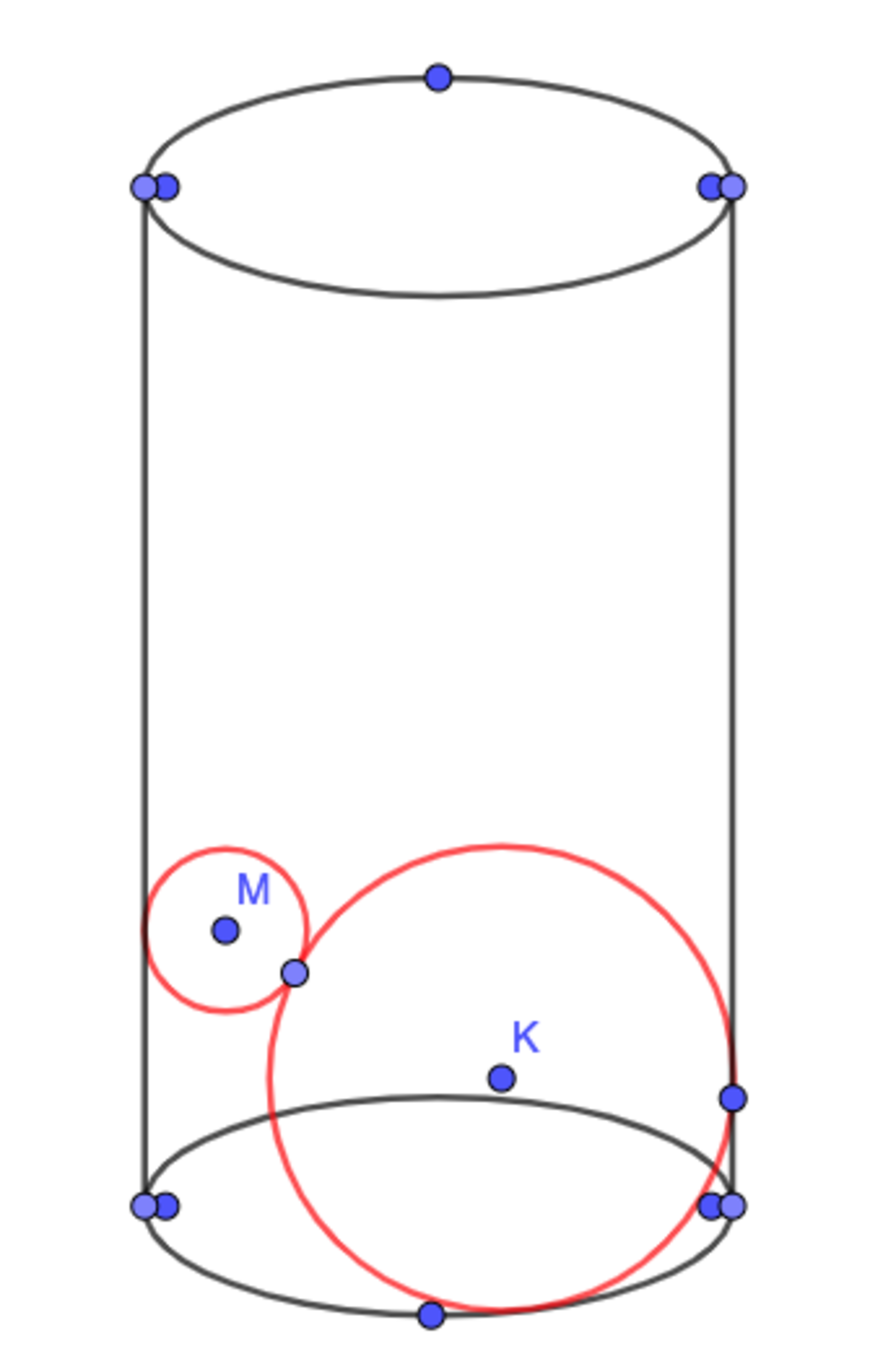A cylinder, which has a diameter of 27 and a height of 30, contains two lead spheres with radii 6 and 9 (
) , with the larger sphere sitting on the bottom of the cylinder , as shown. Water is poured into the cylinder so that it just covers both spheres. The volume of the water required is (the answer contains π).
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Distance between the centres of the spheres is 9 + 6 = 1 5 .
Horizontal distance between them is 1 8 − 6 = 1 2 .
So, vertical distance between them is 1 5 2 − 1 2 2 = 9 .
Therefore height of the top of the smaller sphere above the base of the cylinder is 1 8 + 6 = 2 4 .
Volume of the cylinder upto this height is π × ( 2 2 7 ) 2 × 2 4 = 4 3 7 4 π .
Total volume of the two spheres is 3 4 π ( 6 3 + 9 3 ) = 1 2 6 0 π .
Hence the required volume of water is π ( 4 3 7 4 − 1 2 6 0 ) = 3 1 1 4 π .