Crossing The River
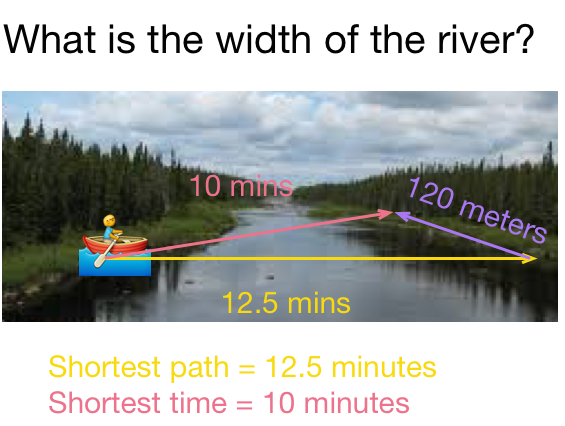
A man crosses a river in a boat. If he crosses the river in minimum time, he takes 10 minutes with a drift . If he crosses the river in the shortest path, he takes 12.5 minutes. Find the width of the river.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the width of the river be ' d '. Let the time taken by the swimmer to cross the river in minimum time be t 1 and that to cross the river via the shortest path is t 2 . Let his horizontal drift for the first case be x . Furthermore, let the speed of the swimmer in still water be v m and that of the river itself, be v r . We'll derive a general result and just plug in the given information to get our answer.
Case 1: Minimum time
For the swimmer to cross the river in minimum time, he must always swim perpendicular to the direction of flow of river. Now, look at the following diagram.
The time taken by man to reach B from O horizontally is only because of the river's velocity, or in other words:
v r = t 1 x
and for vertical motion, it is clear that the distance d and the swimmer's velocity v s can be related as:
v m = t 1 d
Case 2: Shortest distance
For the swimmer to cross the river via the shortest path, he should swim at an angle θ with the river velocity, so as to cancel out the river's horizontal velocity, and allow himself to always travel in the vertical direction.
From the above diagram, it is clear, that to travel in the vertical direction, the following relation must always hold:
v m cos θ = v r
and for vertical motion:
v m sin θ = t 2 d
Now, squaring and adding the last two equations, so as to eliminate θ , and using up the value of v m and v r from the equations formed earlier, we get:
t 1 2 d 2 = t 2 2 d 2 + t 1 2 x 2
or by simplifying:
d 2 = t 1 2 x 2 t 2 2 − t 1 2 t 1 2 t 2 2
and finally:
d = ( t 2 − t 1 ) ( t 1 + t 2 ) x t 2
Now, inserting the given values, i.e. x = 1 2 0 m , t 1 = 1 0 minutes and t 2 = 1 2 . 5 minutes, we get d = 2 0 0 m