A fair game
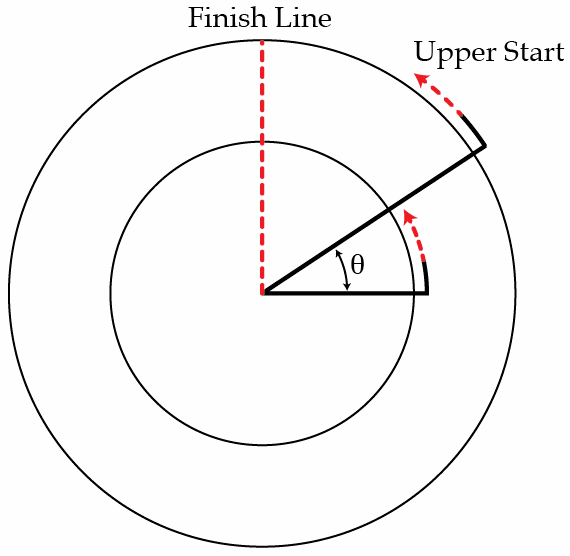
Distance runners often run around an approximately circular trajectory. However, since some runners are running at a larger radius than others, they must be given an advantage in the beginning so that the race is fair.
If the path of the runner running at a greatest radius of 2 0 m is 1 0 0 m long, how far behind in m should the runner at the smallest radius start? The smallest radius is 1 5 m .
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Discussions for this problem are now closed
The circumference of the larger track is 4 0 π ≈ 1 2 5 . 6 6 3 7 , and the circumference of the smaller track is 3 0 π ≈ 9 4 . 2 4 7 7 8 . This means the larger track guy has to run 2 5 . 6 6 3 7 meters less than the full track, and the smaller track guy has to run 5 . 7 5 2 2 2 meters more than the full track.
An initial reaction would be to add these numbers together, but this does not work; you must convert the longer distance to a percentage, then multiply this percentage by the circumference of the shorter track. Without doing this, it's like adding inequivalent units. 12 feet plus 2 inches is not 14 inches.
So, 4 0 π 2 5 . 6 6 3 7 × 3 0 π ≈ 1 9 . 2 4 7 7 8 .
1 9 . 2 4 7 7 8 + 5 . 7 5 2 2 2 = 2 5 meters.
Note: of course, this problem could have been done in exact terms rather than approximated terms, but I find it hard to visualize 4 0 π meters.
Path lengths of both runners are the same, ie 100 m. Consider the arc formed by the path of runner running at greatest radius. this arclength = 100 m. Let length of the arc formed by other runner corresponding to this arc be 'x', then,
x/15 =100/20 ; x=75.
100-75=25 Hence, runner at the smallest radius should start from 25 m behind the other runner.
s=r θ, 100m= 20m x θ, so the value of θ for the outer path is 5rad. Since the race is fair, the distance of the inner path must be 100m, 100m=15m x θ, θ is equal to 6.67rad. the difference in radiant is 1.67rad, so 15m x 1.67rad= 25m
The problem basically reduces down to finding the difference that the outside runner traverses, compared to the inside runner, if they where to start from radially parallel positions.
By doing some preliminary calculations, we notice that the outside runner is not going around the full circumference C B i g of the circle.
C B i g = 2 ⋅ π ⋅ 2 0 ≈ 1 2 5 m but 1 2 5 = 1 0 0
Therefore we can't find the difference by C B i g − C S m a l l .
However, we can use the relationship between the subtended angle and the arc length and radius to solve the problem. The central angle θ is proportional to the arc length S B i g over the radius R B i g :
θ = R B i g S B i g .
Furthermore, there is also an arc, that subtends that same angle, that corresponds to the inside runners path.
θ = R S m a l l S S m a l l .
We can use this relation to find the distance the inside runner travels.
R B i g S B i g = R S m a l l S S m a l l ⇒ 2 0 1 0 0 = 1 5 S S m a l l ⇒ S S m a l l = 7 5
This means, if the runners where to start from radially parallel positions and finish at corresponding points. Then the outside runner would traverse a greater distance. So to make it fair, we can move back the starting point of the inside runner by the difference of the distances.
S B i g − S S m a l l = 1 0 0 − 7 5 = 2 5
The definition of theta is arclength divided by radius or r s = θ
Since theta from the finish line to the upper start line is the same for both circles (not the labeled theta) we know:
r 1 s 1 = r 2 s 2
Plugging in numbers we get
2 0 1 0 0 = 1 5 s 2 = 5
So s 2 = 7 5 . Now for the runner at the smaller radius to be 100 away from the finish line as well he needs to be an additional 25 m away from the finish line making the answer 25.
by ratio and proportion, 1 0 0 2 0 = x 1 5 giving x = 75.
since the runner (who runs in smaller radius) should start running when the remaining distance to finish for the another runner (in larger radius) is equal to the distance for him to run then 100 - 75 = 25 m.
- First of all, let's find circumference of the circle that has 20m radius.
- 2 * π * 20m = 125.66m
- Now Let's find the circumference of the circle that has 15m radius.
- 2 * π * 15m = 94.25m
- From the data we calculated, we can find out the difference of two circumferences :
- 125.66m - 94.25m = 31.42m
- We need to remember that this difference is for the whole circumference. We can find out the difference for 100m by creating simple ratios such as this one:
- 125.66m / 31.416m = 100m / x ---> x=25m
Therefore if the 20m radius path is 100m long, it's difference with a 15m radius path will be 25m long. This means that the shorter path should start 25m behind.
Given: Radius of outer circle is 20 m, Radius of inner circle is 15 m, Total distance 100 m
Find: How far back inner circle runner must start to have both runners cover the same distance.
Solution: For a circle with radius r, and arc length s, and central angle θ : s=r×θ
For outer circle radius 20 m and distance 100 m, angle is 5 radians.
100=20θ θ=5 For inner circle, radius 15 m and distance 100 m, angle is 20/3 radians
100=15θ θ=20/3 Angle difference is 20/3−5=5/3 and by multiplying the angle with the radius of 15, the arc length of 25 is obtained.
s=15∗5/3 s=25
We are given s = r θ where: s = arc length , r = radius .
Solving for θ we have, 1 0 0 = 2 0 θ ⇒ θ = 5
For the smaller radius we have, s = 1 5 ( 5 ) ⇒ s = 7 5
For the two to be equal, the second shall run 1 0 0 − 7 5 = 2 5 m behind the first.
Given: Radius of outer circle is 20 m, Radius of inner circle is 15 m, Total distance 100 m
Find: How far back inner circle runner must start to have both runners cover the same distance.
Solution: For a circle with radius r, and arc length s, and central angle θ : s = r × θ
For outer circle radius 20 m and distance 100 m, angle is 5 radians.
1 0 0 = 2 0 θ
θ = 5
For inner circle, radius 15 m and distance 100 m, angle is 20/3 radians
1 0 0 = 1 5 θ
θ = 2 0 / 3
Angle difference is 2 0 / 3 − 5 = 5 / 3 and by multiplying the angle with the radius of 15, the arc length of 25 is obtained.
s = 1 5 ∗ 5 / 3
s = 2 5