A Familiar Function

Relevant wiki: Fibonacci Sequence

$\begin{aligned} S_n & = \sum_{i=1}^{\lfloor n/2\rfloor}\left[\frac 1{i!} \prod_{k=i+1}^{2i} (n-k)\right] \\ & = \sum_{i=1}^{\lfloor n/2\rfloor} \frac {(n-i-1)!}{i!(n-2i-1)!} \\ & = \sum_{\color{#3D99F6}i=1}^{\lfloor n/2\rfloor} \binom {n-i-1}i & \small \color{#3D99F6} \text{For odd }n= 2m+1 \\ & = {\color{#3D99F6} \sum_{\color{#D61F06}i=0}^{\left \lfloor \frac {n-1}2\right \rfloor} \binom {n-i-1}i} - 1 \\ & = {\color{#3D99F6}F_n} - 1 & \small \color{#3D99F6} \text{where }F_n \text{ is the }n \text{th Fibonacci number.} \end{aligned}$

For $n = 15$ , $1+S_{15} = F_{15} = \boxed{610}$ .

Source: Wikipedia

Rough proof:

The function is equal to $1 + (n-2) + \sum_{a=1}^{n-4} a + \sum_{a=1}^{n-6} {\sum_{b=1}^{a} b} + \sum_{a=1}^{n-8} {\sum_{b=1}^{a} {\sum_{c=1}^{b} c}} +\ldots$ Which is equal to the number of permutations of strings of length n containing the characters "a" and "b", where two b's can't appear next to each other, and the string must begin and end with an "a". Each term is equal to the number of allowed permutations with a certain number of b's included. This set of rules can be represented by a Markov chain: 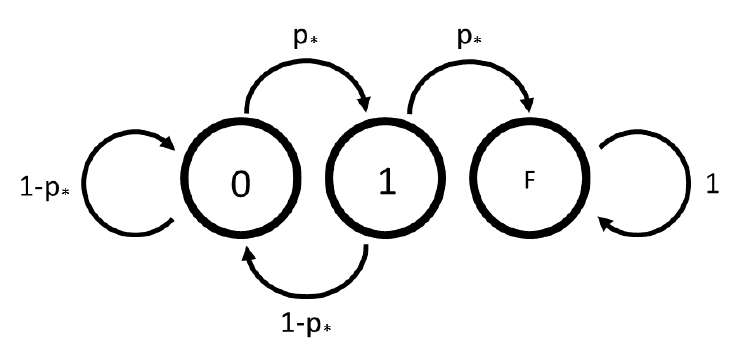Where the total number of permutations as a function of the length n can be expressed as the matrix: $\begin{bmatrix} 1/2 & 1/2&0\\ 1/2 & 0 & 0\\ 0 & 1/2 & 0 \\ \end{bmatrix}^n \cdotp \begin{bmatrix} 0 \\ 2^n \\ 0 \\ \end{bmatrix} = \begin{bmatrix} F(n) \\ a \\ b \\ \end{bmatrix}$ Where the first matrix can be expanded as: $\begin{bmatrix} 0 & \frac{1+\sqrt{5}}{2} &\frac{1-\sqrt{5}}{2}\\ 0 & \frac{-3-\sqrt{5}}{2} & \frac{-3+\sqrt{5}}{2}\\ 1 & 1 & 1 \\ \end{bmatrix} \begin{bmatrix} 1^n & 0 &0\\ 0 & (\frac{1-\sqrt{5}}{4})^n & 0 \\ 0 & 0 & (\frac{1+\sqrt{5}}{2})^n \\ \end{bmatrix} \begin{bmatrix} 1 &1&1\\ \frac{-5+3\sqrt{5}}{10} & \frac{-5+\sqrt{5}}{10} & 0\\ \frac{-5-3\sqrt{5}}{10} & \frac{-5-\sqrt{5}}{10} & 0 \\ \end{bmatrix}$ Using this to solve for F(n), you get:

$F(n)=\frac{(1+\sqrt{5})^n - (1-\sqrt{5})^n}{2^n \sqrt{5}}$ Otherwise known as Binet's formula, which is equal to the Fibonacci sequence for all positive integers. Therefore, the solution of the function at n=15 is equal to the 15th Fibonacci number, 610.