A family of complex integrals

The substitution $y = x^{mn}$ gives $\begin{aligned} I(n,m) & = \; \frac{1}{m^2n^2}\int_0^\infty \frac{y^{\frac1m-1}\,\ln y}{y+1}\,dy \; = \; \frac{1}{m^2n^2}\frac{d}{d\alpha}B(\alpha,1-\alpha)\Big|_{\alpha=\frac1m} \; = \; \frac{1}{m^2n^2}\frac{d}{d\alpha}\Gamma(\alpha)\Gamma(1-\alpha) \Big|_{\alpha=\frac1m} \; = \; \frac{1}{m^2n^2} \frac{d}{d\alpha}\pi\mathrm{cosec}\,\pi\alpha \Big|_{\alpha=\frac1m} \\ & = \; -\frac{\pi^2}{m^2n^2}\mathrm{cosec}\,\tfrac{\pi}{m} \cot \tfrac{\pi}{m} \end{aligned}$ which makes $I(n,2) = 0$ for $n \ge 1$ and $I(3,3) = -\frac{2\pi^2}{243}$ , giving the answer $2 + 2 + 243 = \boxed{247}$ .

In the lemma below we will prove that for all $n \in \mathbb{N}_{\geq1}$ , $m \in \mathbb{N}_{\geq2}$ , $\mathcal{I}(n,m) = -\frac{\pi^2\cos(\pi/m)}{n^2m^2\sin^2(\pi/m)}.$ From this, it automatically follows that $\mathcal{I}(3,3) = -\frac{2\pi^2}{243} \text{ and } \mathcal{I}(n, 2) = 0 \text{ for all } n \in \mathbb{N}_{\geq1}.$ Hence, $a+b+c=2+2+243=\boxed{247}$ .

Lemma : For all $n \in \mathbb{N}_{\geq1}$ , $m \in \mathbb{N}_{\geq2}$ , $\mathcal{I}(n,m) = -\frac{\pi^2\cos(\pi/m)}{n^2m^2\sin^2(\pi/m)}.$ First of all, by substituting $u = x^n$ , we get rid of the first variable of the integral $\mathcal{I}(n,m) = \int_0^\infty \frac{x^{n-1}\log(x)}{x^{nm}+1}\mathrm{d}x = \frac{1}{n^2}\int_0^\infty \frac{\log(u)}{u^m+1}\mathrm{d}u.$ We will now focus on the last given integral, which we will denote by $\mathcal{J}$ .

We define $f: \mathbb{C} \to \mathbb{C}, f(z) = \frac{\log(z)}{z^m+1}$ and $\log: \mathbb{C}\to\mathbb{C}, \log(z) = \log|z| + i\cdot\arg(z)$ , where $-\frac{\pi}{2} < \arg(z) < \frac{3\pi}{2}$ denotes the argument of $z$ . Consider the integral $\oint_\mathscr{C} f(z) \mathrm{d}z,$ over the contour $\mathscr{C}$ going anti-clockwise as seen in the following picture, where $r < 1, R > 1$ and the "diagonal" line is given by $z = \lambda e^{2\pi i/m}$ , with $r \leq \lambda \leq R$ .

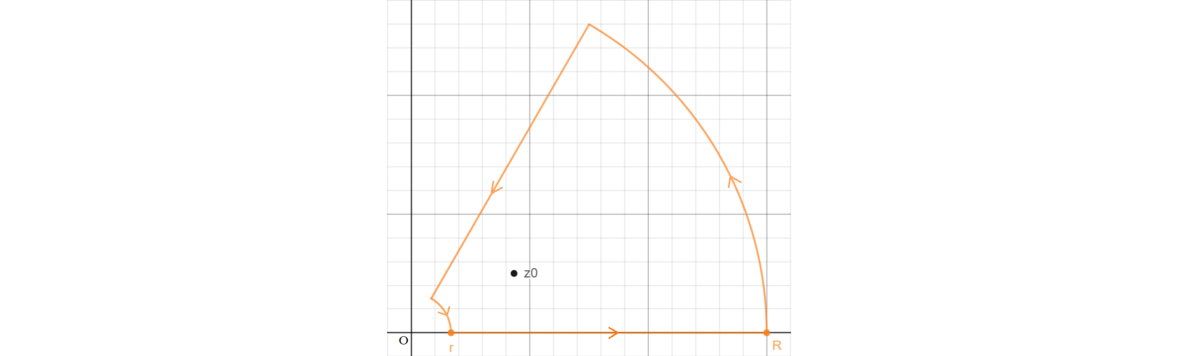
The two parts of the contour which are not represented by lines are part of the circles with center $O$ and radius $R,r$ , respectively. In the picture the point $z_0 = e^{\pi i/m}$ can be seen, which is the only singularity within the contour.

From the definition of the contour, it follows that $\oint_\mathscr{C} f(z) \mathrm{d}z = \mathcal{J} + \int_{\mathcal{C}_R} f(z)\mathrm{d}z + \int_{\mathcal{C}_{2\pi i/m}} f(z)\mathrm{d}z + \int_{\mathcal{C}_r} f(z)\mathrm{d}z,$ where $\mathcal{C}_R, \mathcal{C}_{2\pi i/m}, \mathcal{C}_r$ define the different parts in an obvious way. We will now show that both $\int_{\mathcal{C}_R} f(z)\mathrm{d}z \text{ and } \int_{\mathcal{C}_r} f(z)\mathrm{d}z$ tend to 0 as $R\to\infty, r\to 0$ . For the first integral, observe that $|z^m+1| \geq |z^m|-1$ so that $\left|\int_{\mathcal{C}_R} f(z)\mathrm{d}z\right| \leq \frac{2\pi R}{m} \max\limits_{z\in\mathcal{C}_R} \left|\frac{\log(z)}{z^m+1}\right| \leq \frac{2\pi R}{m} \max\limits_{z\in\mathcal{C}_R} \frac{|\log(z)|}{R^m-1} \leq \frac{2\pi R}{m} \max\limits_{z\in\mathcal{C}_R} \frac{\log(R)+|i\cdot\arg(z)|}{R^m-1} \xrightarrow{R\to\infty} 0.$ The other integral can be dealt with in a similar fashion. Now, note that by the remark in the problem, $\lim_{(r,R)\to(0,\infty)}\int_{\mathcal{C}_{2\pi i/m}} f(z)\mathrm{d}z = -e^{2\pi i/m}\int_0^\infty \frac{\log(R)+2\pi i/m}{R^m+1}\mathrm{d}r = -e^{2\pi i/m}\left(\mathcal{J}+\frac{2\pi^2i/m^2}{\sin(\pi/m)}\right).$ Now, by the Residue theorem, it follows that $\oint_\mathscr{C} f(z) \mathrm{d}z = 2\pi i \cdot \text{Res}_{z=e^{\pi i/m}} \frac{\log(z)}{z^m+1} = 2\pi i \frac{\pi i/m}{me^{\pi i(m-1)/m}} = \frac{2\pi^2}{m^2}e^{\pi i/m}.$ Gathering all information we got so far, we notice that $\mathcal{J} = \frac{2\pi^2}{m^2}\cdot \frac{e^{\pi i /m}+ie^{2\pi i /m}\csc(\pi/m)}{1-e^{2\pi i /m}}.$ Using that $\csc(z) = \frac{2i}{e^{iz}-e^{-iz}}$ , after some algebraic manipulations it can be shown that $\frac{e^{iz}+ie^{2iz}\csc(z)}{1-e^{2iz}} = \frac{e^{iz}+e^{-iz}}{(e^{iz}-e^{-iz})^2} = -\frac{\cos(z)}{2\sin^2(z)}.$ So, $\mathcal{J} = -\frac{\pi^2\cos(\pi/m)}{m^2\sin^2(\pi/m)},$ and we conclude that for all $n \in \mathbb{N}_{\geq1}$ , $m \in \mathbb{N}_{\geq2}$ , $\boxed{\int_0^\infty \frac{x^{n-1}\log(x)}{x^{nm}+1}\mathrm{d}x = -\frac{\pi^2\cos(\pi/m)}{n^2m^2\sin^2(\pi/m)}.}$