A Fermat's Problem

Starting from the given equation, we obtain the equivalent equation

${ (2x-y) }^{ 2 }+{ (x+1) }^{ 2 }=625$

Note that $625={ 25 }^{ 2 }$ . Since $x$ and $y$ are both integers, then the left side of the given equation is the sum of two perfect squares. Since any perfect square is non-negative, then each of these perfect squares is at most $625={ 25 }^{ 2 }$ . The perfect squares from ${ 0 }^{ 2 }$ to ${ 25 }^{ 2 }$ are:

$0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625$

The pairs of perfect squares from this list that have a sum of $625$ are $625 = 625 + 0 = 576 + 49 = 400 + 225$

Therefore, ${ (2x-y) }^{ 2 }$ and ${ (x+1) }^{ 2 }$ equal ${ 25 }^{ 2 }$ and ${ 0 }^{ 2 }$ in some order, or ${ 24 }^{ 2 }$ and ${ 7 }^{ 2 }$ in some order, or ${ 20 }^{ 2 }$ and ${ 15 }^{ 2 }$ in some order. Thus, $2x - y$ and $x + 1$ equal $±25$ and $0$ in some order, or $±24$ and $±7$ in some order, or $±20$ and $±15$ in some order.

Since $x ≥ 0$ , then $x+1 ≥ 1$ , so we need to consider the possibilities that $x+1 = 25, 24, 7, 20, 15$ :

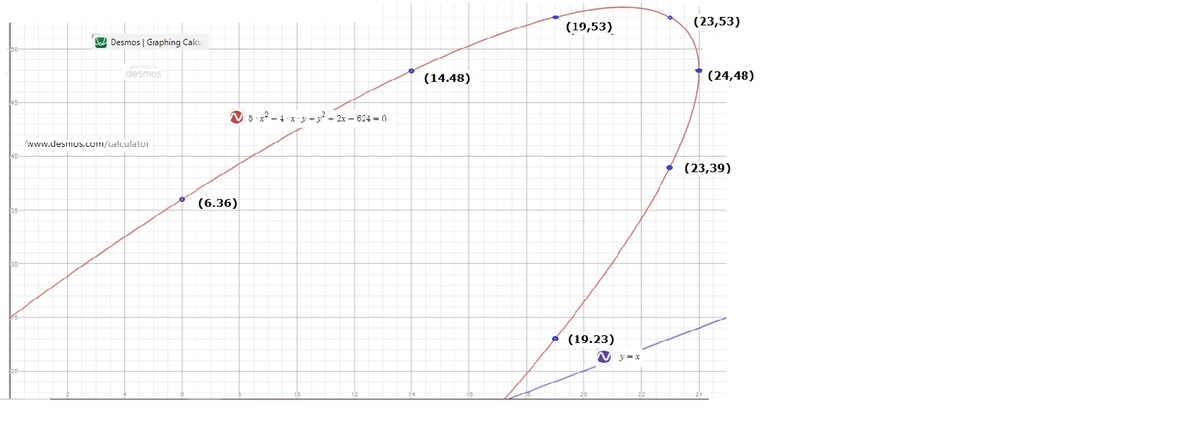
• If $x + 1 = 25$ , then $x = 24$ . If $2x - y = 0$ and $x = 24$ , then $y = 48$ .

• If $x + 1 = 24$ , then $x = 23$ . If $2x - y = 7$ and $x = 23$ , then $y = 39$ ; if $2x - y = -7$ and $x = 23$ , then $y = 53$ .

• If $x + 1 = 7$ , then $x = 6$ . If $2x - y = 24$ and $x = 6$ , then $y = -12$ ; if $2x - y = -24$ and $x = 6$ , then $y = 36$ .

• If $x + 1 = 20$ , then $x = 19$ . If $2x - y = 15$ and $x = 19$ , then $y = 23$ ; if $2x - y = -15$ and $x = 19$ , then $y = 53$ .

• If $x + 1 = 15$ , then $x = 14$ . If $2x - y = 20$ and $x = 14$ , then $y = 8$ ; if $2x - y = -20$ and $x = 14$ , $then y = 48$ .

From this list, the pairs of non-negative integers $(x, y)$ that satisfy the condition $0 ≤ x ≤ y$ are $(x, y) = (24, 48),(23, 39),(23, 53),(6, 36),(19, 23),(19, 53),(14, 48)$ . There are $7$ such pairs.