A Flock Of Herons

Geometry Level 5

Triangles $\Delta ABC$ and $\Delta XYZ$ are Heronian triangles, which are triangles that have integer sides with integer areas.

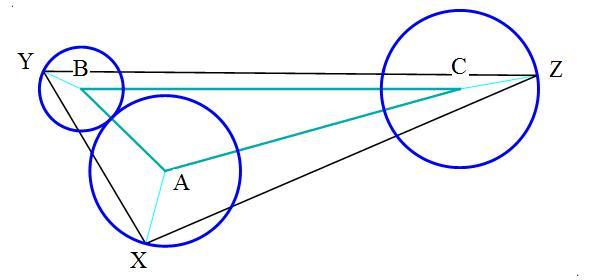
Points $A,B,C$ are centers of circles, the radii of which are

Radius of circle $A=1092=2^2\cdot 3\cdot 7\cdot 13$
Radius of circle $B=608=2^5\cdot 19$
Radius of circle $C=1140=2^2\cdot 3\cdot 5\cdot 19$

The sides of triangle $\Delta ABC$ are

$AB=1700=2^2\cdot 5^2\cdot 17$
$BC=5491=17^2\cdot 19$
$CA=4437=3^2\cdot 17\cdot 29$

Triangle $\Delta XYZ$ has the maximum area of any triangle (Heronian or not) that has one vertex on the circumference of each of the circles $A,B,C$

Let $\dfrac { \Delta XYZ }{ \Delta ABC } =\dfrac { p }{ q }$

be the ratio of the areas of triangles $\Delta XYZ$ and $\displaystyle \Delta ABC$

where $p,q$ are $4$ digit co-prime integers. The difference $p-q$ is a $4$ digit prime number.

Find that prime number.

For your convenience, area of triangle $\displaystyle \Delta ABC$ works out to

$3261654=2\cdot 3^3\cdot 11\cdot 17^2\cdot 19$

Note: Triangle $\Delta XYZ$ as drawn in graphic does not have the maximum area

Also, as you solve this, you'll come across more Herons. A helpful hint, I hope.

The answer is 6131.

1 solution

Michael Mendrin
Sep 15, 2014

Triangle $\Delta XYZ$ is a $8:15:17$ right triangle, and centers $B$ and $C$ are on sides $XY$ and $XZ$ respectively. A necessary and [and maybe not--see Calvin below] sufficient condition that Triangle $\Delta XYZ$ has the maximum area is that tangents at $X,Y,Z$ are parallel to lines $YZ,XZ,XY$ respectively. The worked out values for the lengths are as follows

$AX=1092={2 }^{ 2 }\cdot { 3 }\cdot 7\cdot 13$
$AB=1700={2 }^{ 2 }\cdot { { 5 }^{ 2 } }\cdot 17$
$AC=4437={ 3 }^{ 2 }\cdot 17\cdot 29$
$AD=1188={ 2 }^{ 2 }\cdot { 3 }^{ 3 }\cdot 11$
$XB=2584={ 2 }^{ 3 }\cdot 17\cdot 19$
$XC=4845=3\cdot 5\cdot 17\cdot 19$
$BC=5491={ 17 }^{ 2 }\cdot 19$
$BD=1216={ 2 }^{ 6 }\cdot 19$
$DC=4275={ 3 }^{ 2 }\cdot { 5 }^{ 2 }\cdot 19$
$XY=3192={ 2 }^{ 3 }\cdot 3\cdot 7\cdot 19$
$XZ=5985={ 3 }^{ 2 }\cdot 5\cdot 7\cdot 19$
$YZ=6783={ 3 }\cdot 7\cdot 17\cdot 19$

It also works out that all these triangles are Heronians, with areas given

$\Delta BAX = 663936 = { 2 }^{ 7 }\cdot 3\cdot 7\cdot 13\cdot 19$
$\Delta BDA = 722304 = { 2 }^{ 7 }\cdot { 3 }^{ 3 }\cdot 11\cdot 19$
$\Delta BDX = 1386240 = { 2 }^{ 8 }\cdot { 3 }\cdot 5\cdot { 19 }^{ 2 }$
$\Delta CAX = 2334150 = 2\cdot { 3 }^{ 3 }\cdot { 5 }^{ 2 }\cdot 7\cdot 13\cdot 19$
$\Delta CDA = 2539350 = 2\cdot { 3 }^{ 5 }\cdot { 5 }^{ 2 }\cdot 11\cdot 19$
$\Delta CDX = 4873500 = { 2 }^{ 2 }\cdot { 3 }^{ 3 }\cdot { 5 }^{ 3 }\cdot {19}^{2}$
$\Delta ABC = 3261654 = { 2 }\cdot { 3 }^{ 3 }\cdot 11\cdot { 17 }^{ 2 }\cdot 19$
$\Delta XBC = 6259740 = { { 2 }^{ 2 } }\cdot { 3 }\cdot 5\cdot { 17 }^{ 2 }\cdot { 19 }^{ 2 }$
$\Delta XYZ = 9552060 = { { 2 }^{ 2 } }\cdot { { 3 }^{ 3 } }\cdot 5\cdot { 7 }^{ 2 }\cdot { 19 }^{ 2 }$
$BCZY = 3292320 = { { 2 }^{ 5 } }\cdot { { 3 } }\cdot 5\cdot { 19 }^{ 3 }$ (This is a quadrilateral with integer sides, long sides parallel)

Thus $\dfrac { \Delta XYZ }{ \Delta ABC } =\dfrac { 9310 }{ 3179 }$ and the answer is the prime number $6131$

So, indeed, there’s a flock of herons.

I agree that the condition "Triangle $XYZ$ has the maximum area is that tangents at $X, Y, Z$ are parallel to lines $YZ, ZX, XY$ respectively" is necessary. However, I do not think it is sufficient.

For one, you could end up with the minimum area instead. Alternatively, you end up with a local max/min, but not the global max.

E.g. Take a case of 3 circles where $A,B$ are tangential at $P$ , and this tangent is also tangential to $C$ at $Q$ . Then $PPQ$ is a triangle which satisfies your conditions, and has 0 area.

Calvin Lin Staff - 6 years, 9 months ago

Calvin, I knew you were going to bring up that objection. Well, I originally tried to be more precise in the wording, but it came out too wordy. It's a messy subject. How to you define the points "that are on the outside furthest from each other"? Worse, when you try to find triangles of minimum areas, you can run into trouble if the circles aren't in "nice" places.

Anyway, you are absolutely right, but I'm not sure how to word it more correctly without adding another confusing paragraph.

I originally started out with a different problem, but even though I had the solution, it was extremely difficult, so I revised it to one to have "nice" integers, and, well, I ended up with this. I wanted to see if it was even possible at all.

Michael Mendrin - 6 years, 9 months ago

Another way of stating that condition would be that for altitudes feet to be furthest from corresponding vertices they need to pass through circles' centres thus maximizing the triangle area.

Maria Kozlowska - 5 years, 9 months ago

A Flock Of Herons

The answer is 6131.

1 solution

0 pending reports