2 × 4 5 ∘ = 9 0 ∘
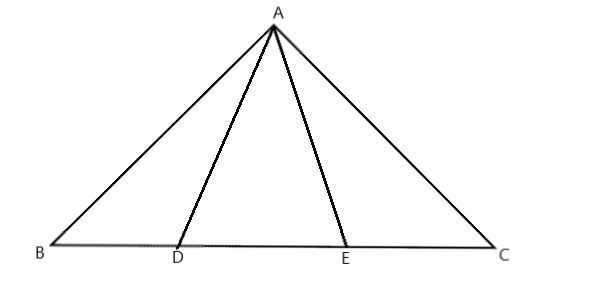
In △ A B C , ∠ A = 9 0 ∘ , A B = A C , and points D and E are on B C such that ∠ D A E = 4 5 ∘ .
If B D = 2 0 and E C = 2 1 , then find the area of △ A B C .
The answer is 1225.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
A B = A C = x so E D = 2 x − 4 1 and the area sought will be 2 x 2
By the law of cosines on each of the outer triangles
A D 2 = x 2 − 2 0 2 x + 4 0 0 and A E 2 = x 2 − 2 1 2 x + 4 4 1
Which allows the law of cosines on the inner triangle
E D 2 = A D 2 + A E 2 − 2 A D ⋅ A E cos 4 5
( 2 x − 4 1 ) 2 = x 2 − 2 0 2 x + 4 0 0 + x 2 − 2 1 2 x + 4 4 1 − 2 x 2 − 2 0 2 x + 4 0 0 x 2 − 2 1 2 x + 4 4 1 cos 4 5 simplifies to
x 4 − 4 1 2 x 3 + 1 7 2 2 0 2 x − 1 7 6 4 0 0 = 0
( x 2 − 4 1 2 x + 4 2 0 ) ( x 2 − 4 2 0 ) = 0
x = 6 2 or x = 3 5 2 or x = 2 1 0 5 or x = − 2 1 0 5
Since E D > 0 , x > 2 4 1 and the only solution that fits is x = 3 5 2 meaning the area is 3 5 2 = 1 2 2 5
Hint: Fold the triangle(the creases are A D and A E ) so B and C meets at a point F . You will discover that △ D E F is a right triangle, so D E = 2 0 2 + 2 1 2 = 2 9