A Fourier Problem
What is the sum of all Fourier coefficients of the Fourier series of the following function f which is defined for all real x and has period 2? Note that on [ − 1 , 1 ] , f corresponds to the absolute value function.
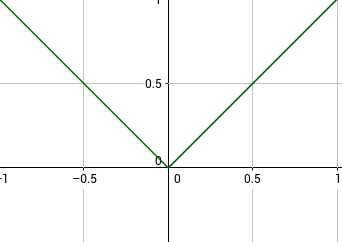
If the Fourier series corresponds to the standard form of the Fourier series as illustrated below, enter the sum of all coefficients a and b as your aswer.
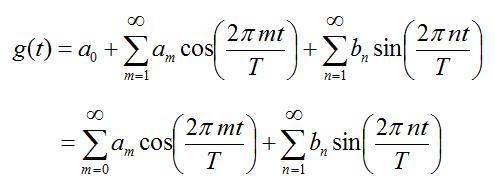
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Indeed. It is true that the fourier series for even functions have no sin ( 2 n π t ) terms. While saying that "odd functions cannot sum up to even functions" is a good intuitive reason, that isn't always true since − x + x = 0 gives 2 odd functions that sum to an even function.
To show that the coefficients are 0, apart from evaluating the coefficients in the conventional way, we can also use the facts that
- The odd functions cos ( 2 n π t ) are linearly independent
- The sum of (countably many) odd functions is still odd
- The only function that is both even and odd is the 0 function
to conclude that if ∑ a i ( cos 2 π i t ) is an even function, then (by 3 ) the sum is 0 and hence (by 1) a i = 0 .
Log in to reply
Generally, if we're talking about Fourier coefficients, we already know that they're uniquely defined by the function. Under that assumption, here's another argument for the same.
Then, since f ( x ) is even, it equals its own even part: f ( x ) = 2 f ( x ) + f ( − x ) and T defined by T g ( x ) = 2 g ( x ) + g ( − x ) annihilates every odd function, so applying it to a Fourier series will annihilate all the sine terms.
By the uniqueness of the Fourier coefficients, no sine terms show up in the Fourier series.
I first solved it in the conventional way, but the sipmlicity of the answer made me look for an elegant solution that I will describe here. First, notice that f is an even function which implies that all coefficients of the sine terms in the Fourier series are 0 (because sin(x) is odd). Thus, we only need to find the sum of the cosine coefficients, and notice that evaluating f(0) makes, independently of m, all cosines 1 (because cos(0) = 1). Thus, f(0) is equal to the sum of all cosine coefficients and since f(0) = 0, the answer is 0.