A fractal triangle
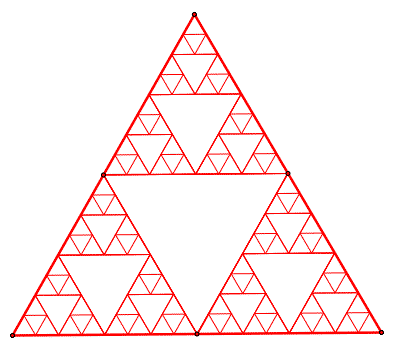 The figure above is
Sierpinski triangle
, It turns out the moment of inertia can be calculated. If the moment of inertial through its center and perpendicular to the plane can be written as
. What is the value of
, where
is the side length and
and
are co-prime positive integers?
The figure above is
Sierpinski triangle
, It turns out the moment of inertia can be calculated. If the moment of inertial through its center and perpendicular to the plane can be written as
. What is the value of
, where
is the side length and
and
are co-prime positive integers?
Not an original problem
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider the next smaller triangle.
It has mass 3 M and length 2 l . So its Moment of Inertia about its center of mass is I s = B A 3 M 4 l 2
Moment of Inertia of smaller part about the center of mass of the bigger part is :- I s C M = B A 1 2 M l 2 + 3 M 1 2 l 2 I s C M = B A 1 2 M l 2 + 3 6 M l 2 The total Moment of Inertia about the center of mass is:- I C M = 3 I s C M ⟹ B A M l 2 = 3 I s C M Solving this, we get:- B A = 9 1