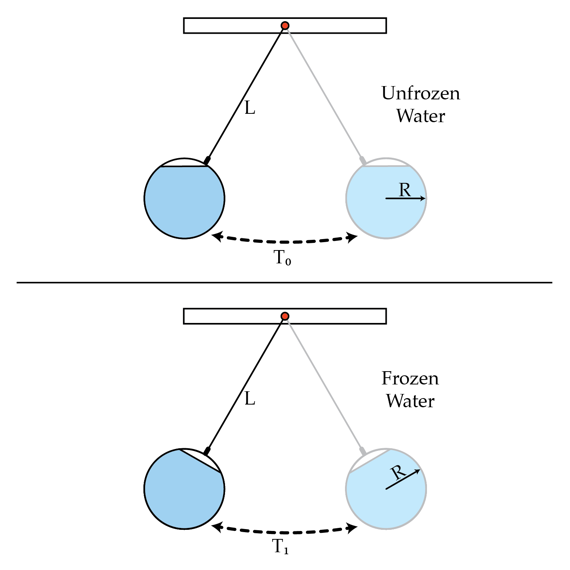
A frozen pendulum

Before freezing, the water can move freely in the container and the kinetic energy of the pendulum includes only the translational energy of the center of mass. Therefore, its period of small oscillations is the same as a simple pendulum's: $T_0=2\pi\sqrt{\frac{L}{g}}$

After freezing, the system became a rigid body which possesses also the rotational energy. Because of the spherical shape of the container, the moment of inertia of the pendulum about the pivot point is $I=I_0+mL^2=\frac{2}{5}mR^2+mL^2$ , where $m$ is the mass of the pendulum. The new period of small oscillations is $T_1=2\pi\sqrt{\frac{I}{mgL}}=2\pi\sqrt{\frac{L(1+\frac{2R^2}{5L^2})}{g}}$

Finally, we receive the ratio $\frac{T_1}{T_0}=\sqrt{1+\frac{2R^2}{5L^2}}$

If $\frac{L}{R}=2$ then $\frac{T_1}{T_0}\approx1.05$

The key observation is the following: When the container with water ( in liquid phase) oscillates, the system behaves as a simple pendulum. Note that the liquid does not rotate around its center of mass and therefore the energy of the system is simply $E= \frac{Mv^{2}}{2}+ Mg h$ where v and h are the velocity and height of the center of mass. The last expression suggests that even though we are describing an object of finite dimensions, its energy coincides with that of a point-like mass. Consequently, the system can be described as a simple pendulum. On the other hand, when the water freezes, the system becomes rigid and it should be described as a physical pendulum. Then the total energy of the system must include the rotational kinetic energy, that is $E=\frac{Mv^{2}}{2}+ \frac{ I \omega^{2}}{2}+Mg h$ where $I=\frac{2}{5} MR^{2}$ is the moment of inertia with respect to the center of mass. Now we can apply the well-known formulas $T_{0}=2\pi \sqrt{\frac{L}{g}}$ for a simple pendulum and
$T_{1}=2\pi \sqrt{\frac{I+ML^{2}}{MgL}}$ for a physical pendulum. Combining the above equations we obtain: $\frac{T_{1}}{T_{0}}= \sqrt{1+\frac{2}{5} \frac{R^{2}}{L^{2}}}=1.05.$