A game out of this world
In a traditional game of Tic-tac-toe on a
3
×
3
board, players need to place
3
marks on either a horizontal, vertical, diagonal line to win. One can count there are
8
winning lines on this
3
×
3
board.
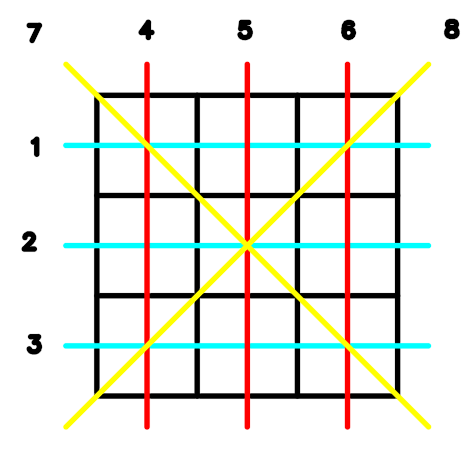 But if someone add a twist to this game, namely playing on a bigger board
1
0
×
1
0
and requiring
5
marks in a line to win, there would be
1
9
2
winning lines. For example, all the lines below are winning lines.
But if someone add a twist to this game, namely playing on a bigger board
1
0
×
1
0
and requiring
5
marks in a line to win, there would be
1
9
2
winning lines. For example, all the lines below are winning lines.
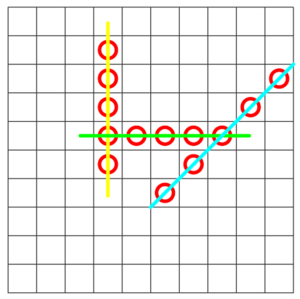 If we go to 3 dimensions by playing on a
7
×
7
×
7
or
7
3
cube and need
4
marks in line to win, there would be
1
5
1
6
winning lines.
If we go to 3 dimensions by playing on a
7
×
7
×
7
or
7
3
cube and need
4
marks in line to win, there would be
1
5
1
6
winning lines.
If we go to the 6th dimension, play on a 1 2 6 cube and need 5 marks in a line to win, how many winning lines are there?
Note: though you don't need a calculator on the process to the final calculation, you might need one once you get there.
Bonus: derive a formula to compute number of winning lines for a game that needs b marks to win on a n cube, where a is the cube's side length and n is the number of dimensions.
The answer is 239452160.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Here's how to derive the formula for the general case. Once we have it, just plug all numbers into a calculator for the specific case this problem asked.
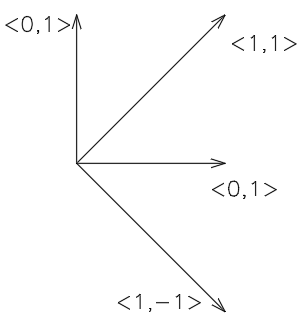
Two marks are on a same line if their displacement vector is a multiple of a winning vector (this winning vector is a term I just made up). Now, on a 2-dimensional board, regardless of the size, there are 4 winning vectors:
⟨
1
,
0
⟩
,
⟨
0
,
1
⟩
,
⟨
1
,
1
⟩
,
⟨
1
,
−
1
⟩
 For a 3-dimensional cube, regardless of the size, there are 13 winning vectors. Some of which are:
⟨
0
,
1
,
−
1
⟩
,
⟨
1
,
1
,
0
⟩
,
⟨
1
,
0
,
−
1
⟩
For a 3-dimensional cube, regardless of the size, there are 13 winning vectors. Some of which are:
⟨
0
,
1
,
−
1
⟩
,
⟨
1
,
1
,
0
⟩
,
⟨
1
,
0
,
−
1
⟩
Note that for the sake of convenience, I'm indicating vector components in pointy brackets instead of i ^ , j ^ or k ^ terms.
Note that even though ⟨ 1 , 0 , − 1 ⟩ and ⟨ − 1 , 0 , 1 ⟩ are 2 different vectors but since they are just opposite, they both have the same line of action so they are counted as one winning vector. That makes some sense because a winning line is the same no matter where you count the marks from (up to down, down to up, left to right, right to left, etc.)
So here's a rule of writing winning vectors in any number of dimensions so none of those are the same: the first non-zero component must be 1 , any component after that can be either 1 , 0 or − 1 . For example ⟨ 0 , 0 , 1 , 0 , − 1 , 1 , 0 , . . . , 1 ⟩ .
Now we figured out winning vectors, let's put the a n cube we are playing on in a coordinate system with n number of axes, we can put marks on points with coordinates of non-zero integers up to a . For example ( 8 7 , 1 , 9 , 3 1 , a − 5 0 0 , . . . , a − 1 0 0 1 , a ) .
We need b marks in a row to win. Let's denote a winning vector as w , point C is a point with coordinates of integers from 0 to a . We need to put marks in points C + w , C + 2 w , C + 3 w , ..., C + b w to win, assuming they are all inside the cube of course. That means all the points I just listed must have non-zero integer coordinates up to a . However, we only need make sure none of C + w 's coordinates is 0 and none of C + b w 's coordinates is larger than a
The hardest part is over, we now know what to do. For every single winning vector, we count how many points it can make a winning line with. I will be brief from now on because the rest isn't hard. In shorts, we will need the binominal theorem and this identity:
u 0 v m − 1 + u 1 v m − 2 + u 2 v m − 3 + . . . + u m − 1 v 0 = u − v u m − v m
Recall we are playing on a a n board and need b marks in a line.
For winning vectors existing in n dimensions: ⟨ 1 , . . . . . . . ⟩ , we have a 0 ( a − b + 1 ) ( 3 a − 2 b + 2 ) n − 1 winning lines
For winning vectors existing in n − 1 dimensions: ⟨ 0 , 1 , . . . . . . . ⟩ , we have a 1 ( a − b + 1 ) ( 3 a − 2 b + 2 ) n − 2 winning lines
For winning vectors existing in n − 2 dimensions: ⟨ 0 , 0 , 1 , . . . . . . . ⟩ , we have a 2 ( a − b + 1 ) ( 3 a − 2 b + 2 ) n − 3 winning lines
...................................................
For winning vectors existing in 1 dimension: ⟨ 0 , 0 , 0 , . . . . . . . , 1 ⟩ , we have a n − 1 ( a − b + 1 ) ( 3 a − 2 b + 2 ) 0 winning lines
We used binominal theorem for the previous calculations, now add all those terms together using the identity I just gave, we have the final answer:
* On a a n board that need b marks in a line, there are 2 ( 3 a − 2 b + 2 ) n − a n winning lines. *
For the question, put in a = 1 2 , n = 6 , b = 5 , we have 2 3 9 4 5 2 1 6 0 winning lines
How can I forgive myself. I did the same but answer was very big because my untrustworthy eyes 👀 saw 4 lines instead of 5.😋
For a general a n cube with b marks to win. With coordinates ( x 1 , x 2 , . . . x n ) , let x i ˉ be a unit vector in the i t h dimension. Winning lines are multiples of ∑ k i ∗ x i ˉ , where k i = − 1 , 0 , or 1 . Excluding the case where all k i = 0 , as this is a point/stationary line.
If k i = 0 , at the starting point of a winning line x i can take a values. If k i = ± 1 , x i can take a − b + 1 values between within [ 1 , a − b + 1 ] or [ b , a ] respectively.
There are 2 r ∗ ( r n ) possible vectors with exactly r non-zero k i , as they can each be ± 1 , (excluding r = 0 as this is a point not a line).
Hence in total there are ∑ ( r n ) a n − r [ 2 ( a − b + 1 ) ] r = ( a + 2 ( a − b + 1 ) ) n − a n .
This counts each line twice, one time in each direction. Hence there are a total of 2 ( 3 a − 2 b + 2 ) n − a n possible winning lines.
Plugging in a = 1 2 , n = 6 , b = 5 , we get 2 2 8 6 − 1 2 6 = 2 3 9 4 5 2 1 6 0 .
Note to author: Question could use numbers such that the answer becomes easily computable without a calculator, eg a = 1 0 , n = 6 , b = 6 , or something to do with the form of the answer, eg it can be broken into ( 7 6 − 3 6 ) 2 1 1 = ( 3 4 3 − 2 7 ) ( 3 4 3 + 2 7 ) 2 1 1 = ( 2 2 ∗ 7 9 ) ( 2 ∗ 5 ∗ 3 7 ) ( 2 1 1 ) = 2 1 4 ∗ 5 ∗ 3 7 ∗ 7 9