A Gaussian Revolution
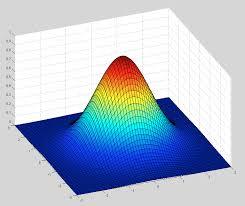
Find the volume comprised between the function z ( r , θ ) = e − r 2 and the x y plane.
Bonus : Use this result to find the value of ∫ − ∞ ∞ e − x 2 d x
The answer is 3.14159.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The volume asked for is very straightforward using cylindrical coordinates and has a value of π (see @Tom Engelsman 's solution.)
The result can be used to compute ∫ − ∞ ∞ e − x 2 d x . We need to express the volume integral using cartesian coordinates:
∫ − ∞ ∞ ∫ − ∞ ∞ e − ( x 2 + y 2 ) d x d y = ∫ − ∞ ∞ e − x 2 d x ⋅ ∫ − ∞ ∞ e − y 2 d y = ( ∫ − ∞ ∞ e − x 2 d x ) 2 = π ⟹ ∫ − ∞ ∞ e − x 2 d x = π
The volume in question can be computed via the double integral in cylindrical coordinates:
V = ∫ 0 2 π ∫ 0 ∞ e − r 2 r d r d θ = π .
The given function is positive definite, so the volume is just V = ∫ x y − p l a n e e − r 2 d S .
V = ∫ 0 2 π ∫ 0 ∞ r e − r 2 d r d θ
For those wondering where the factor r comes from, it always appears when we swich to polar coordinates, it is called the Jacobian determinant for polar coordinates. If we have the coordinate mapping
{ x = r cos θ y = r sin θ , then J = [ ∂ r ∂ x ∂ r ∂ y ∂ θ ∂ x ∂ θ ∂ y ] = [ cos θ sin θ − r sin θ r cos θ ] and det J = r cos 2 θ + r sin 2 θ = r .
V = ∫ 0 2 π d θ ⋅ ∫ 0 ∞ r e − r 2 d r
= 2 π ⋅ ∫ 0 ∞ d − 2 1 e − r 2
= 2 π ⋅ ( − 2 1 e − ∞ − ( − 2 1 e 0 ) )
= 2 π ⋅ ( 0 + 2 1 )
= π