A generalization of Butterfly Theorem?
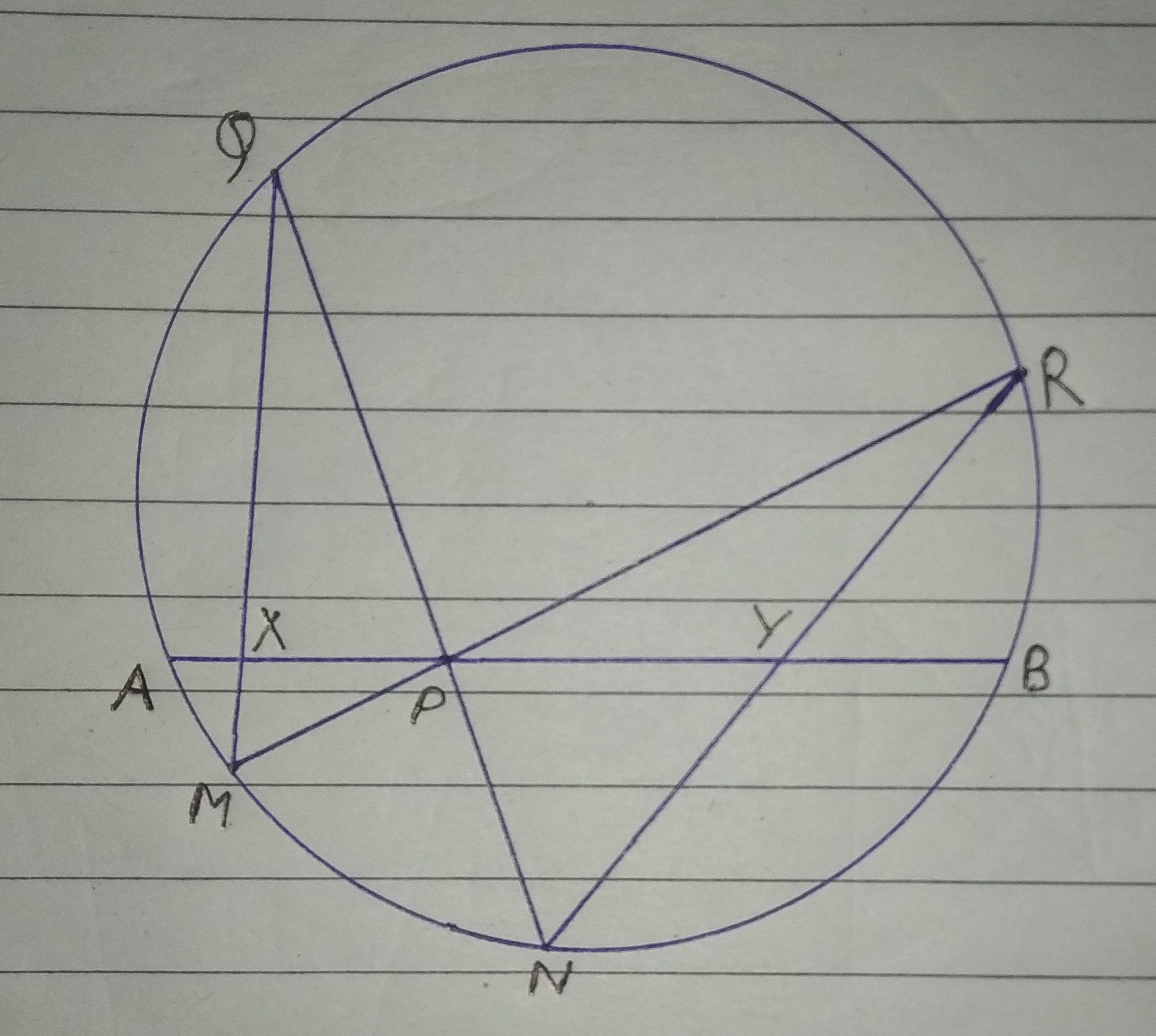
In the above figure, Chords A B , M R and N Q intersect in a Circle at Point P . Q M and R N intersect with A B at Points X and Y respectively. If A P = 8 , P B = 1 5 , find X P 1 − Y P 1 . If your answer is of the form b a , where a and b are positive coprime integers, enter your answer as a + b .
The answer is 127.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Assuming the question is correct and that the answer is the same for any M R and N Q through point P , pick M and Q so that they are both on A and pick R and N so that they are both on B . Then X is also on A and Y is also on B so that X P = A P = 8 and Y P = P B = 1 5 .
Then X P 1 − Y P 1 = 8 1 − 1 5 1 = 1 2 0 7 , so a = 7 and b = 1 2 0 and a + b = 1 2 7 .
To prove it without the assumption, place the diagram on a coordinate graph such that P is at the origin and A and B are on the x -axis. Let a = A P and b = P B , let c be the shortest distance between the center of the circle to segment A B , let M R have a slope of m 1 so that its equation is y = m 1 x and let Q N have a slope of m 2 so that its equation is y = m 2 x .
Then the circle has a center of ( 2 b − a , c ) and its radius r is the distance between this point and ( b , 0 ) , so that r 2 = c 2 + 4 ( a + b ) 2 . The equation of the circle is then ( x − 2 b − a ) 2 + ( y − c ) 2 = c 2 + 4 ( a + b ) 2 .
Combining the circle equation and y = m 1 x gives an x -coordinate for R of R x = 2 ( m 1 2 + 1 ) b − a + 2 m 1 c + ( b − a + 2 m 1 c ) 2 − 4 a b ( m 1 2 + 1 ) and a x -coordinate for M of M x = 2 ( m 1 2 + 1 ) b − a + 2 m 1 c − ( b − a + 2 m 1 c ) 2 − 4 a b ( m 1 2 + 1 ) . Combining the circle equation and y = m 2 x gives an x -coordinate for N of N x = 2 ( m 2 2 + 1 ) b − a + 2 m 2 c + ( b − a + 2 m 2 c ) 2 − 4 a b ( m 2 2 + 1 ) and a x -coordinate for Q of Q x = 2 ( m 2 2 + 1 ) b − a + 2 m 2 c − ( b − a + 2 m 2 c ) 2 − 4 a b ( m 2 2 + 1 ) . Note that M x + R x = m 1 2 + 1 b − a + 2 m 1 c , Q x + N x = m 2 2 + 1 b − a + 2 m 2 c , M x R x = m 1 2 + 1 − a b , and Q x N x = m 2 2 + 1 − a b .
The equation of the line through R N is y − m 1 R x = R x − N x m 1 R x − m 2 N x , and when y = 0 , x = m 1 R x − m 2 N x R x N x ( m 1 − m 2 ) = Y P . Similarly, the equation of the line through Q M is y − m 2 Q x = Q x − M x m 2 Q x − m 1 M x , and when y = 0 , x = m 2 Q x − m 1 M x Q x M x ( m 2 − m 1 ) = − X P .
Therefore, X P 1 − Y P 1 = Q x M x ( m 1 − m 2 ) m 2 Q x − m 1 M x − R x N x ( m 1 − m 2 ) m 1 R x − m 2 N x = M x N x Q x R x ( m 1 − m 2 ) N x Q x R x m 2 − M x N x R x m 1 − M x Q x R x m 1 + M x N x Q x m 2 = m 1 − m 2 1 ( ( M x R x M x + R x ) m 2 − ( Q x N x Q x + N x ) m 1 ) , and using the relationships for M x , N x , Q x , and R x above, this simplifies to X P 1 − Y P 1 = a 1 − b 1 .
In this problem, a = 8 and b = 1 5 , so X P 1 − Y P 1 = 8 1 − 1 5 1 = 1 2 0 7 . Therefore, a = 7 , b = 1 2 0 , and a + b = 1 2 7 .
See Haruki's lemma here.