A generalization of Gossard perspector and X(110)

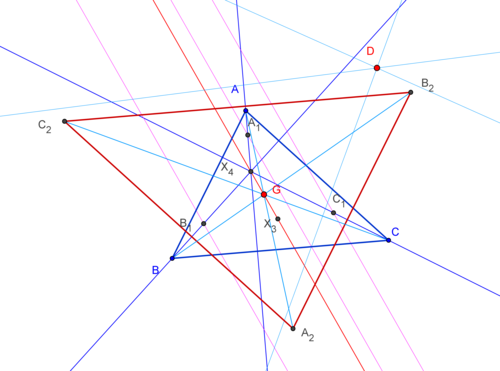Let ABC be a triangle, H is the orthocenter of the triangle ABC. Denote A1,B1,C1 lie on HA,HB,HC. Such that HA1/HA=HB1/HB=HC1/HC=k. d a be the line through A1 and parallel with Euler line meet AB,AC at A b, A c respectively. Define B a,B c,C a, C b cyclically. A2B2C2 is the triangle created by the Euler line of three triangles AAbAc, BBcBa,CCaCb. 1-A 2B 2C 2 and ABC are two similar triangle, and them have the same Euler line 2-A 2B 2C 2 are perpective with ABC, the perpector be a point lie on Euler line, if k=0 then the perpector is Gossard perspector 3-Reflection of thee lines d a,d b,d c in BC,CA,AB respectively are concurrent be a point lie on the X(3)X(110) 4-d a also is the Euler line of the triangle with a vertex is A, two line AB,AC, and A1 is the orthocenter, (d b,d_c similar)