A Geometery
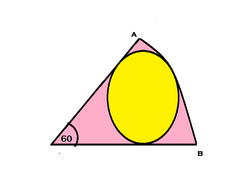 AB is a sector of a sixth of a circle
AB is a sector of a sixth of a circle
The circle is inscribed to it
What is the ratio of the pink area to the yellow area?
If your answer is , enter a+b
THIS QUESTION IS NOT ORIGINAL
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let O be the center of the pink circle, C be the center of the yellow circle and P be the point of tangency of the yellow circle to radial segment O B . Also, let the radius O B of the pink circle be R .
Letting the radius C P of the yellow circle be r , we have that triangle Δ O C P is a right triangle with ∠ C O P = 3 0 ∘ and hypotenuse O C = R − r . Therefore
sin ( 3 0 ∘ ) = R − r r ⟹ 2 1 = R − r r ⟹ R − r = 2 r ⟹ r R = 3 .
Now the yellow area is π r 2 and the pink area is 2 1 ∗ R 2 ∗ 3 π − π r 2 , and thus the ratio of the pink area to the yellow area is
π r 2 2 1 ∗ R 2 ∗ 3 π − π r 2 = 6 1 ∗ ( r R ) 2 − 1 = 6 3 2 − 1 = 2 1 .
Thus a + b = 1 + 2 = 3 .