Observable Planets
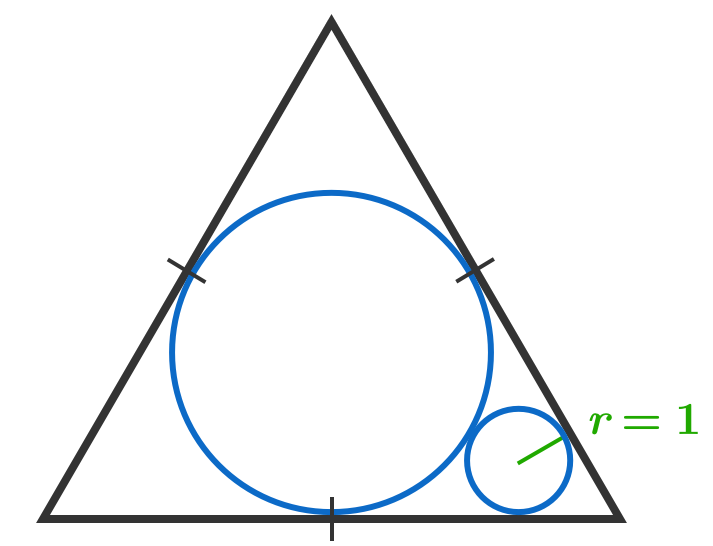
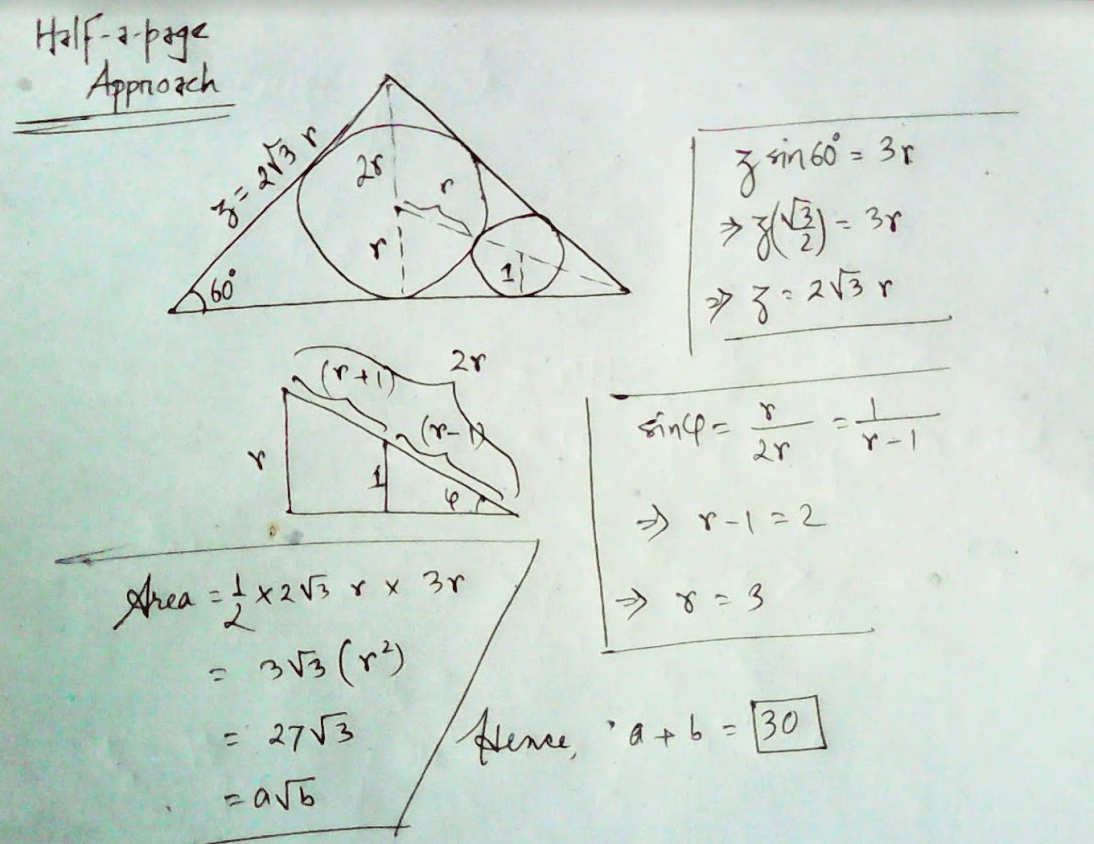
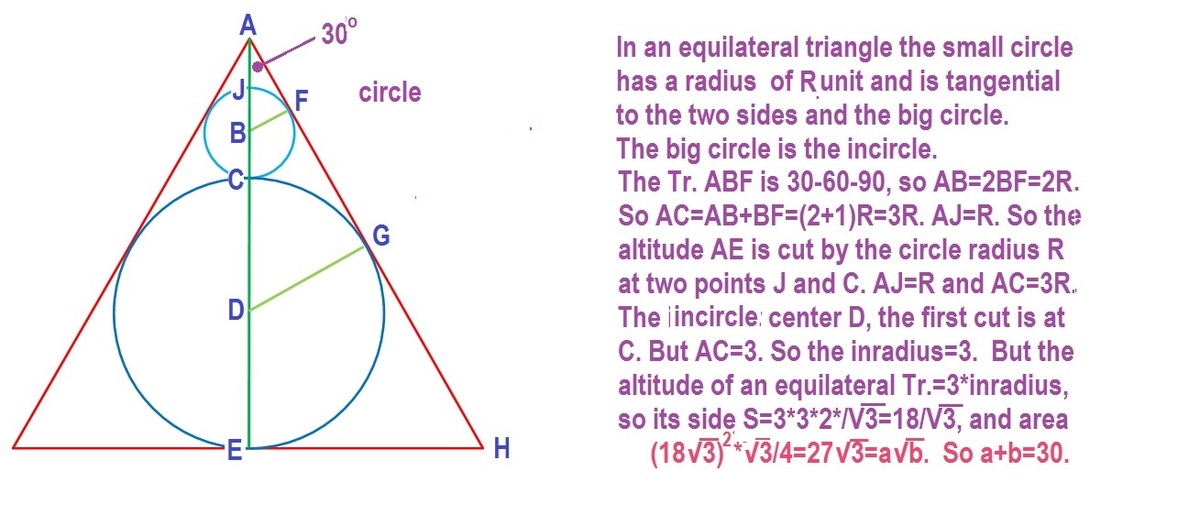
A circle is inscribed in an equilateral triangle. A smaller circle is drawn such that it is tangent to two sides of the triangle as well as the larger circle.
The area of the equilateral triangle is a b , where a and b are positive integers with b square-free. Find a + b .
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution ,+1! Can you tell me how did you upload the picture acc. To question , it is not always available, do you create it ? And one more thing , how to write in colour text ? Please help , thank you.!
Log in to reply
I drag and dropped the picture in Microsoft Paint. And then worked on it there. Please feel free to ask any question. For color I am typing in color. Just put your cursor over it to see how. Or go to top right corner and press on the three lines. Press Toggle LaTex in the dialog box. Come back to see how LaTex is written. Go back an press again to restore.
H
o
w
a
r
e
y
o
u
?
.
O
R
I
a
m
f
i
n
e
.
...(\ )-this space and back slash for space in between the words.
I press at the end three spaces and ENTER to go to the next line.
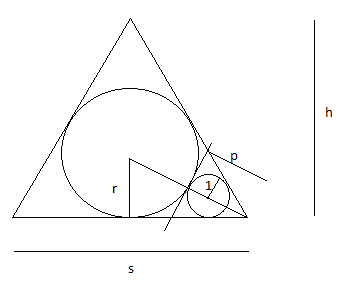h
=
tan
(
6
0
)
∗
s
/
2
=
2
(
3
)
s
r
=
tan
(
3
0
)
∗
s
/
2
=
6
(
3
)
s
h
=
3
r
p
=
3
2
r
+
p
=
h
2
3
h
+
3
=
h
h
=
9
s
=
6
(
3
)
A
=
2
s
h
=
2
7
(
3
)
a
=
2
7
,
b
=
3
a
+
b
=
3
0
p.s. as you can see, the trick is noticing that the big circle is in the big triangle, as the small circle is in the small triangle.
Just learn Latex and your solution will be more effective.
Log in to reply
I can write in Latex, you know! Like, y = ± 2 5 − x 2 But, the problem is I can't draw in Latex. So, when I have to put in images my solution writing gets mediocre.
Log in to reply
Drawing is not difficult. I use Microsoft Paint. You can also use Microsoft word. In insert, press shape. There are others who use geogebra free online. Do learn drawing. It will greatly help you. After you have finished your drawing, save as JPEG. on desktop. In Brilliant box for solution press third tab. It will take you to your laptop screen. Go to where your drawing is stored and press open. Some of your teachers to may be able to help. With best wishes for your progress.