A geometric problem, part II
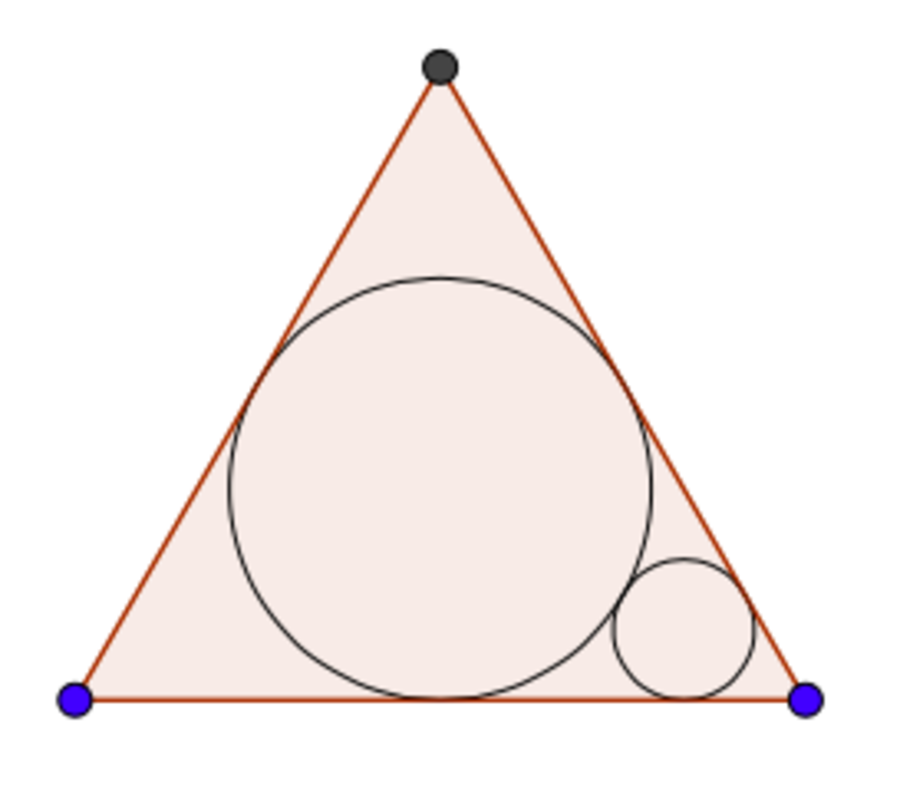
You have a circle (circle 1) inscribed in an equilateral triangle. Then, you construct another circle (circle 2) that is tangent to two sides of the triangle and to circle 1. Then, you construct another circle (circle 3) that is tangent to two sides of the triangle and to circle 2. Then you construct another circle (circle 4) that is tangent to two sides of the triangle and to circle 3. Then you keep doing this infinitely. Now, not only do you do this for one angle of the triangle, but you repeat the same process for the other two angles of the triangle.
By doing the above, you get an infinite number of circles. If the radius of the circle 2 is 1, and if the area covered by all of those circles can be represented in the form b a π , where a and b are coprime positive integers, find a + b .
The answer is 107.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
What is GP?
Log in to reply
GP stands for geometric progression.
can you please explain the last step
Why did you multiply by 3?
r 2 = 1 r n + 1 = 3 r n A n = π r n 2 A T = A 1 + 3 ∑ k = 2 ∞ A k = 8 9 9 π \ 9 9 + 8 = 1 0 7
Why did you multiply by 3?
Log in to reply
total area = area of 1st circle + 3( area of 2nd + area of 3rd + area of 4th...) because the shrinking circles extend in three vertices
Each circle has 1/3 the radius of the last, so the area decreases at a rate of 1/9. The first circle (ignoring the center one) has an area of pi. We know that the value of an infinite sum is the first term divided by the difference of 1 and the rate. Thus, the area in one leg is pi/(8/9). Multiply by 3, because this sum is only for the circles going to one angle, and add the area of the largest circle.
First we shall find the relationship between the radius of a circle and the length of the side.
Let the radius be r , then the length of the side would be given by s = 2 3 r .
Now, observe that the radius of a circle decreases with a common ratio (from circle 1 to circle 2, from circle 2 to circle 3 etc). Our objective is to find this common ratio.
Let us consider a special case, when the biggest circle has radius 1. Then the equilateral triangle has side 2 3 and the distance from a vertex to the centre of the circle is 2. Also, the height of the triangle is 3. Hence, we have this infinite GP:
2 ( 1 + r 1 + r 2 1 + ⋯ ) = 3 1 + r 1 + r 2 1 + ⋯ = 2 3 r − 1 1 = 2 3 r = 3
Hence, we can conclude that each subsequent circle's radius will be one third of the radius of the previous circle.
Now let us go back to the question. Circle 2 has radius 1, so circle 1 has radius 3. The total sum of areas is then: 9 π + 3 π ( 1 2 + 3 1 2 + 3 2 1 2 + ⋯ ) = 8 9 9 π