A Geometry Problem
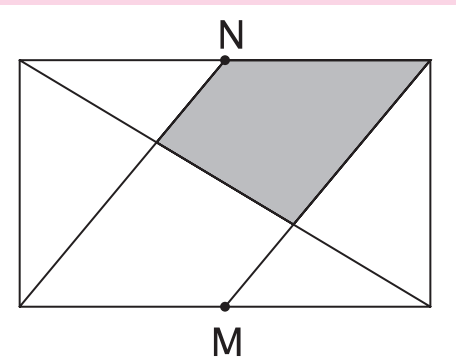 In the image above, the rectangle have an area of
1
2
0
m
2
.
The points M and N are the middle points in their respective segments.
What is the area from the grey region?
In the image above, the rectangle have an area of
1
2
0
m
2
.
The points M and N are the middle points in their respective segments.
What is the area from the grey region?
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I am not aggreed . pl explain it.
Let x and y be the length and the breadth of the rectangle respectively.So xy=120 _(1). Now 2 * (grey area)=a parallelogram's area _ _ (2) ,the area of the parallelogram=( x/2) * y(as M and N are midpoints)=xy/2 ,now putting it in (2), 2 * (area of grey area)=xy/2 or area of grey area=xy/4 or area of grey area=120/4 {from (1)} so area of grey area=30 m^2
If you cut the rectangle in half in the middle and move the little grey triangle sticking out on the left to the bottom part to complete the bigger triangle, you will notice that it results in a triangle that is 1/4 the area of the rectangle. Therefore, 120/4 = 30.
Note that the area of twice the gray region (a parallelogram) is obviously half the area of the rectangle. Therefore, the area of the gray region is half of half the area of the rectangle, or 1 2 0 ÷ 4 = 3 0 m 2 .