Slightly inflated square
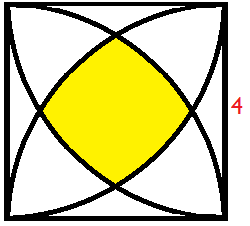 The figure above consists of 4 identical intersecting quadrants inside a square of side 4.
The area of the shaded region can be expressed as
b
a
π
+
c
−
d
e
for positive integers
a
,
b
,
c
,
d
with
e
with
a
and
b
are relatively coprime, and
e
is square free.
The figure above consists of 4 identical intersecting quadrants inside a square of side 4.
The area of the shaded region can be expressed as
b
a
π
+
c
−
d
e
for positive integers
a
,
b
,
c
,
d
with
e
with
a
and
b
are relatively coprime, and
e
is square free.
Evaluate the value of a + b + c + d + e .
The answer is 54.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
@Keil Cerbito on the second line it should be A subscript(AFED)
Log in to reply
thanks for correcting my solution @Joshua Daniel . Actually I had some minor mistakes there, the area that I am talking about on the 2nd line is the area of Sector AEGD.
area of AEGDA = pi/3 (4^2) but you wrote pi/6(4^2)
Log in to reply
Good day Sir @Ravi Nelluri . If you recall the formula for getting the Area of a Sector, it should be A = 2 1 θ r 2 wherein θ = 6 0 ° = 3 π and r = 4 . Substitute to the equation, we will get A = 2 1 ( 3 π ) ( 4 ) 2 = 6 π ( 4 ) 2 = 3 8 π
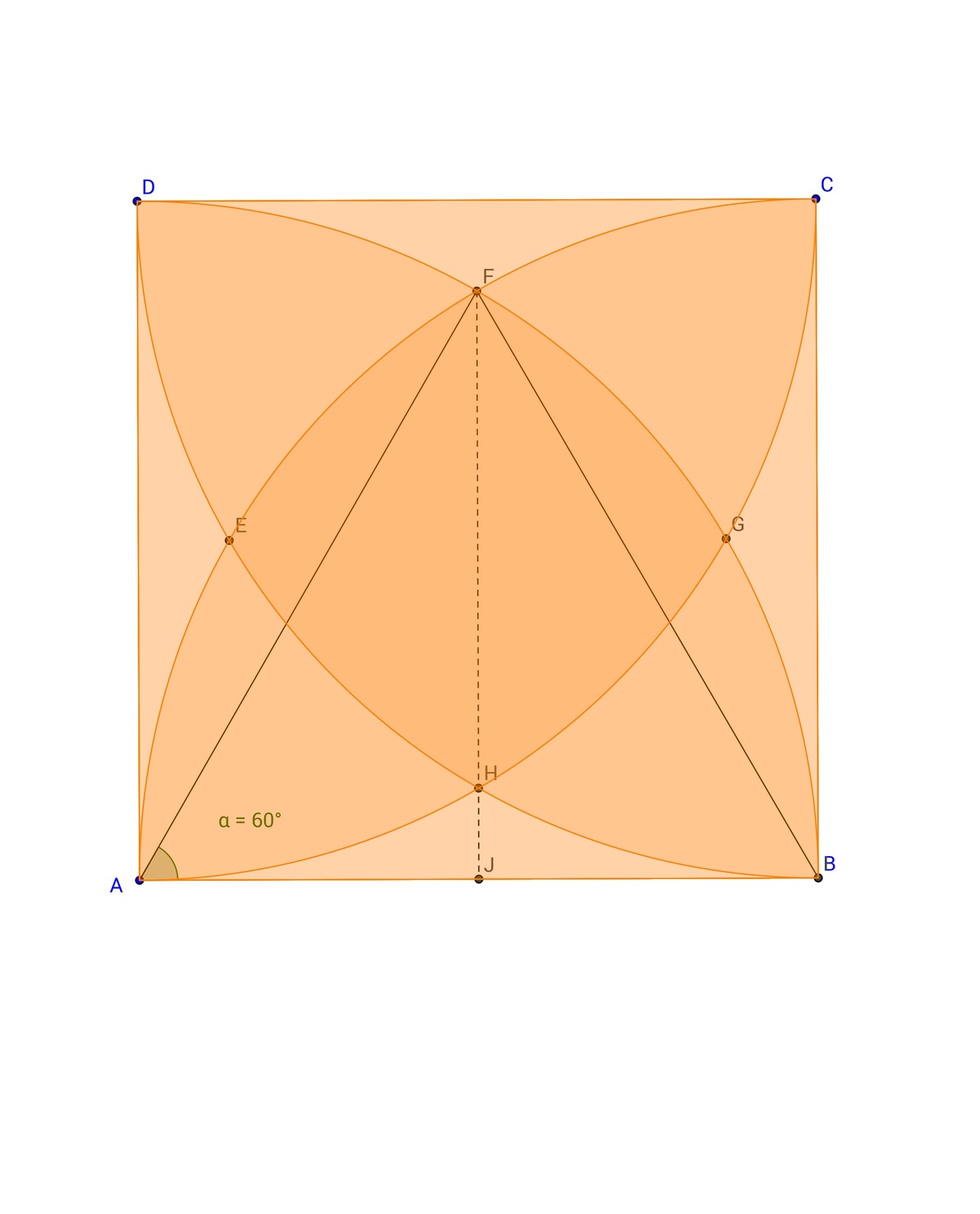
We can calculate the area given by the intersection of the four quadrants as the sum of : 4 A r e a D F C + 2 A r e a D B − A r e a A B C D = A r e a E F G H
Consider the notation as the area enclosed by the lines (No matter if they are curved) that connect the given points corresponding the image above. We call the side of the square r . Then:
A r e a D B = w ⇒ 4 π r 2 × 2 − w = r 2 ⇒ A r e a D B = 2 π r 2 − r 2
In order to calculate the area of D F C we note that triangle Δ A B F is equilateral . So its area is :
2 r 3 × 2 1 × r = 4 r 2 3
The sum of the area of two circular sectors of 6 0 ∘ is: 3 π r 2
The sum of the area of two quadrants is: 2 π r 2
Then the area of D F C is:
r 2 − ( 2 π r 2 − ( 3 π r 2 − 4 r 2 3 ) ) = r 2 − 6 π r 2 − 4 r 2 3
Finally, the generalized form of the area in common of the 4 quadrants is:
A r e a E F G H = x ⇒ x = 2 ( 2 π r 2 − r 2 ) + 4 ( r 2 − 6 π r 2 − 4 r 2 3 ) − r 2
= 3 π r 2 + r 2 − r 2 3
Substituting r, we get:
3 1 6 π + 1 6 − 1 6 3
So the answer is:
1 6 + 3 + 1 6 + 1 6 + 3 = 5 4
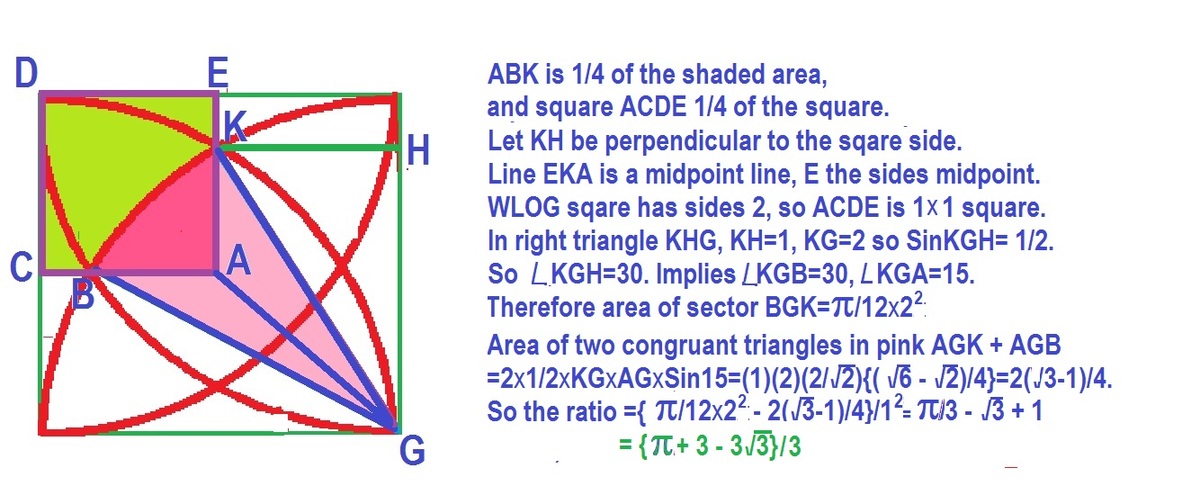 On 6th May 2016 I had answered almost the same equation but square side of 1 instead of 4 as it is here "Blue area by Alan Enrique Ontiveros ".
On 6th May 2016 I had answered almost the same equation but square side of 1 instead of 4 as it is here "Blue area by Alan Enrique Ontiveros ".
The above is the copy of that solution. Since the square here has side 4, the required area is:-
4
2
∗
3
π
+
3
−
3
3
=
3
1
6
+
1
6
−
1
6
3
=
b
a
∗
π
+
c
−
d
3
.
So a+b+c+d+e=16+3+16+16+3=54.
This is the fifth time almost the same equation has appeared.
Bob Kadylo below too has same thing to say.
At the end of January 2016, I did a problem called "Area Of Overlapping Leaves" - Geometry Level 3 - which currently awards 60 points. Lots of detailed beautiful colored solutions I learned from - that were different from the way I did it - but I love that. Anyway, here is the result: 3 a 2 ( π + 3 − 3 3 )
I just applied that general result to this question using "a=4" and multiplied 3 1 6 into the brackets.
Yes 54: Using the notation in Keil Cerito's diagram: Take A as the origin, G has co-ordinates (√12,2). Then 4 x (Int - 2(√12-2)) where Int is the area under the curve x^2+y^2 = 4^2 from 2 to √12! It works! (Also interesting that the value of Int is 1/3 of the area of the quarter circle.)
Moderator note:
Your solution is quite hard to follow. Adding additional details would make it easier to read.
How can one determine the coordinates of G? (e.g. did you use the fact about equilateral triangles? did you use a graphing software?) How can one determine the area of Int? (e.g. did you approximate the area? did you use a graphing software?)
Is there any reason why Int is 1/3 the area of the quarter circle, or is that a happy coincidence?
Set the origin of a system of coordinates at the center of the square. Using the circumferences' equations centered at the vertices V 1 = ( 2 , 2 ) ; V 2 = ( 2 , − 2 ) ; V 3 = ( − 2 , − 2 ) and V 4 = ( − 2 , 2 ) one may find the intersection between the circumferences of V 1 and V 2 and integrate the function of V 2 over the interval [ 2 − 1 2 , 0 ] (i. e. from the intersection to the origin). This is a quarter of the shaded region, thus we multiply the value achieved by four and hence the answer.

A A F E C D A = 4 π ( 4 2 ) = 4 π
A A E G D A = 6 π ( 4 2 ) = 3 8 π
A A F E A = 6 π ( 4 2 ) − 2 ( 4 2 ) sin ( 6 0 ) = 3 8 π − 4 3
A D G E C D = A A F E C D A − A A E G D A − A A F E A
A D G E C D = 4 π − 3 8 π − ( 3 8 π − 4 3 ) = 3 − 4 π + 4 3
A E F G H E = A s q u a r e − 4 A D G E C D
A E F G H E = 4 2 − 4 ( 3 − 4 π + 4 3 )
A E F G H E = 3 1 6 π + 1 6 − 1 6 3
t h e r e f o r e :
a = 1 6 ; b = 3 ; c = 1 6 ; d = 1 6 ; e = 3
a + b + c + d + e = 1 6 + 3 + 1 6 + 1 6 + 3 = 5 4