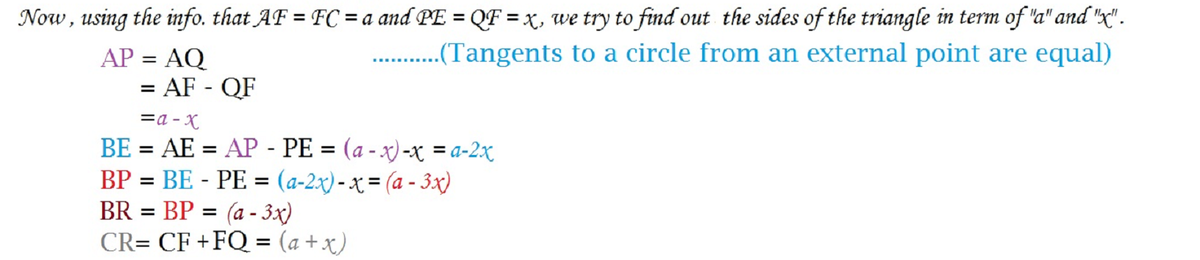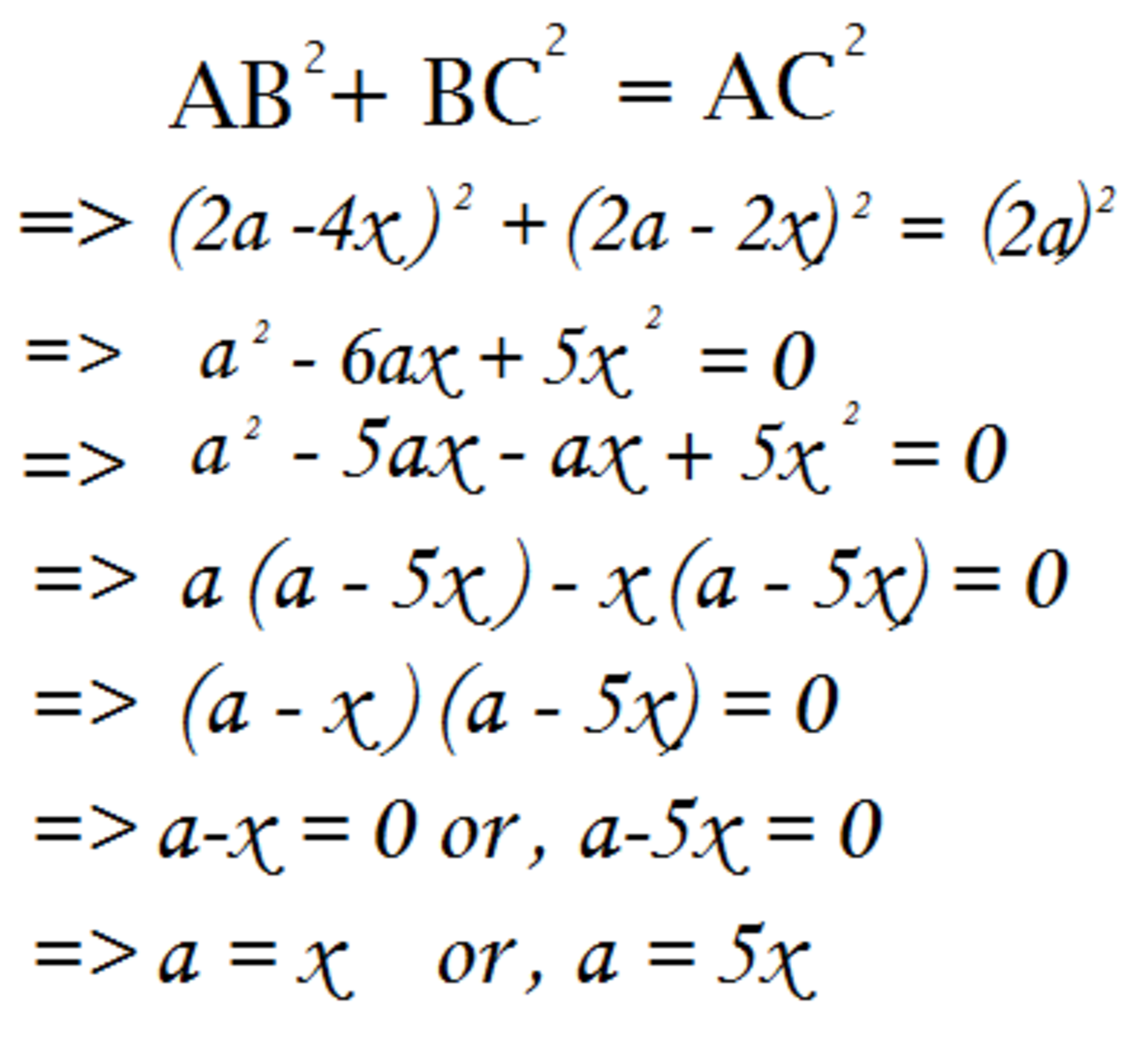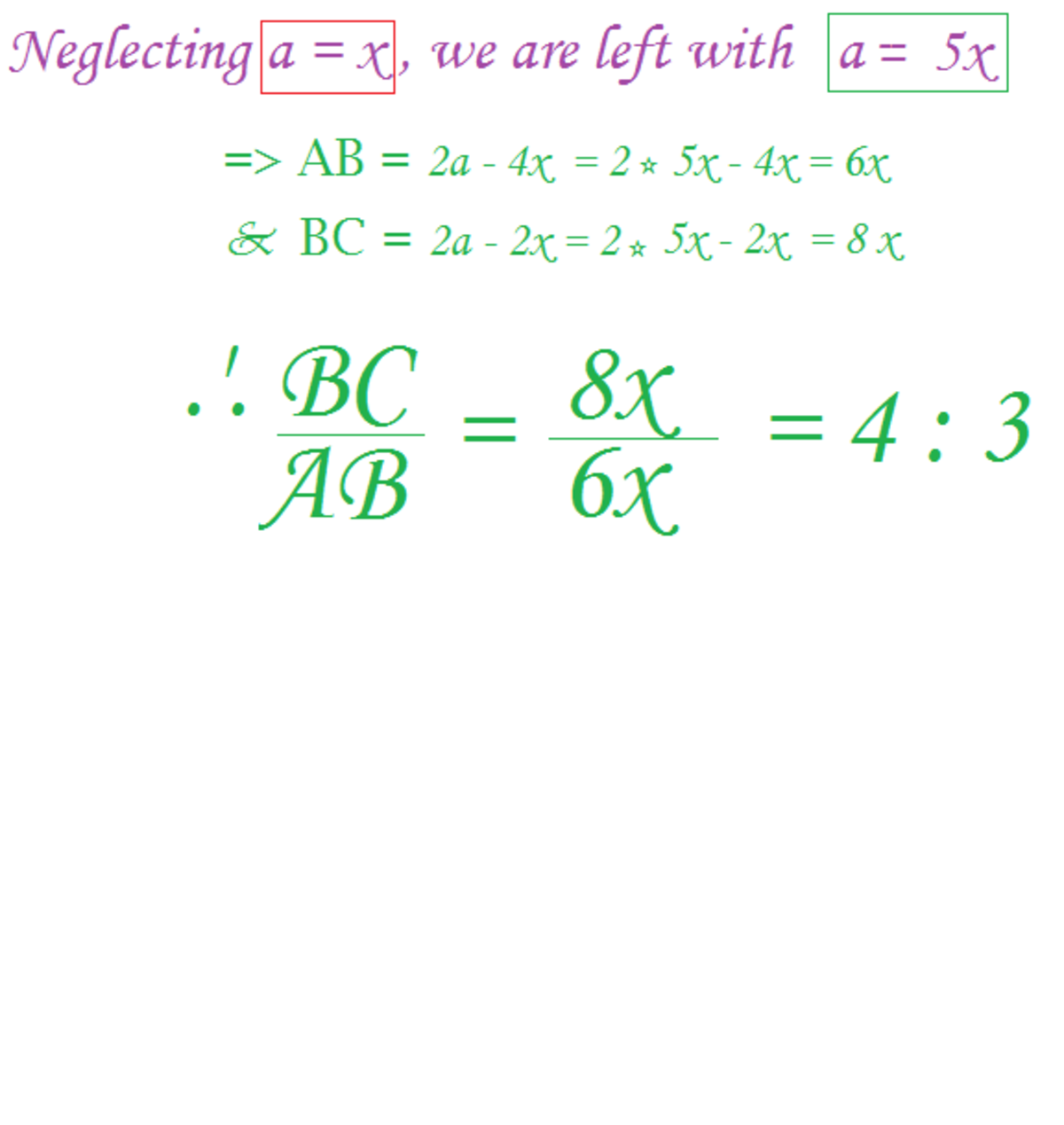Is this information enough?
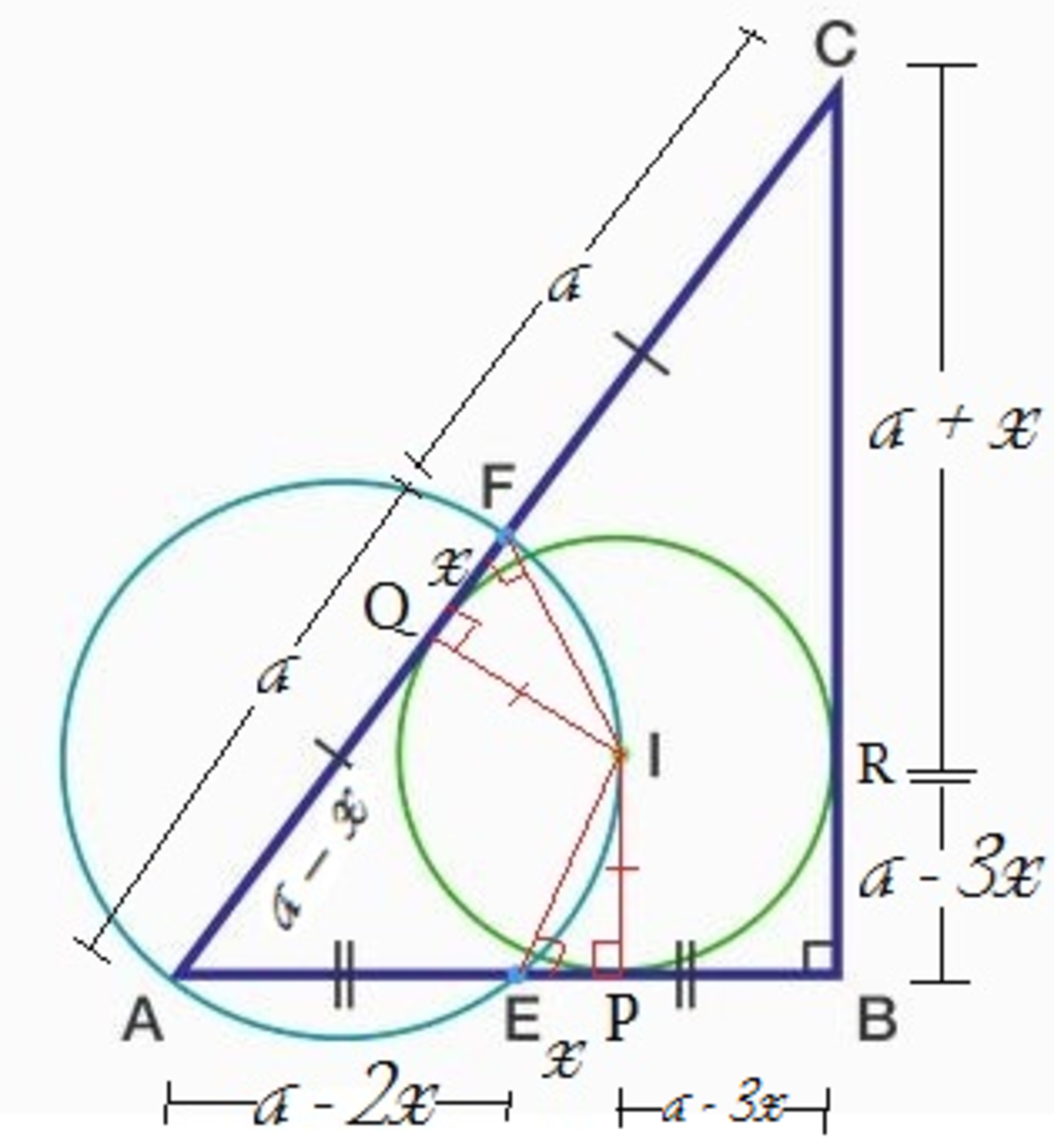
Let A B C be a triangle in which A B = A C . Suppose the orthocenter of the triangle lies on the incircle. If the value of B C A B can be expressed as b a , where a and b are coprime positive integers , entre your answer as a + b .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Construct points D , E , F on B C , A C , A B respectively such that A D ⊥ B C , B E ⊥ A C , C F ⊥ A B . Without loss of generality, let D ( 0 , 0 ) , C ( 1 , 0 ) , B ( − 1 , 0 ) . Let point O be the orthocentre and let the inradius be r . This means that G ( 0 , 2 r ) . Finally let A ( 0 , a ) .
Now, we get the equation of B A to be y = a x + a . This implies that the equation of C F is y = − a 1 x + a 1 . We know that G lies on C F and has x coordinate 0, so subbing in x = 0 , we get G = ( 0 , a 1 ) = ( 0 , 2 r ) ⇒ a = 2 r 1 .
We also know that the area of triangle is given by A D × B C ÷ 2 = a = 2 r 1 . Now, we shall find another way to obtain the area so we can get an equation and solve for r . It is also evident that the area of the triangle is given by B C × r ÷ 2 + A B × r = r + r a 2 + 1 = r + 2 4 r 2 + 1 . Equating, we have r + 2 4 r 2 + 1 = 2 r 1 r 4 r 2 + 1 + 2 r 2 = 1 2 r 2 − 1 = − r 4 r 2 − 1 4 r 4 − 4 r 2 + 1 = 4 r 4 + r 2 5 r 2 = 1 r = 5 1 ⇒ a = 2 5 Since A C = a 2 + 1 , we have A C = 2 3 and thus, B C A C = 2 2 3 = 4 3 and the answer is 7.
this problem appeared in inmo 2016. so please see the solution either from the official site or from aops