Circle the circle

Geometry Level 3

There are two circles. One with centre A [say circle A] of radius 10 cm and one with center C [say circle C] whose radius can be varied with the help of a point B which lies on the circumference of the circle with center A.

The point B is bound to move only on the circumference of the circle A. And the point C stays at one point and cannot move.

What will be the minimum diameter of the circle C so that the circle A is completely inside the circle C?

40 40 40 π 40\pi 20 20 20 π 20\pi

Abhay Tiwari by Abhay Tiwari , 28, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Abhay Tiwari
Apr 20, 2016

As we vary the radius of circle C, we get this: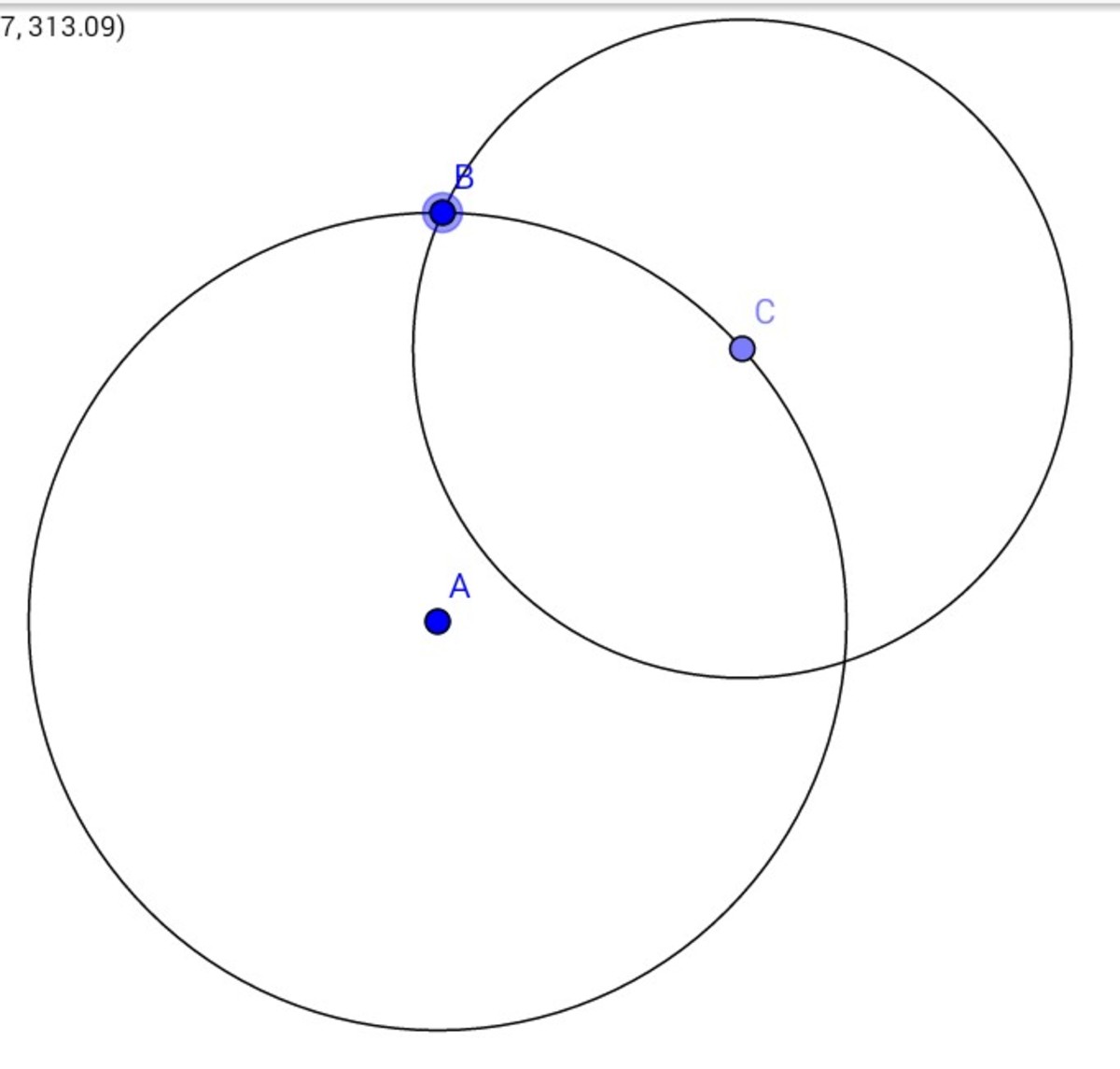

And finally this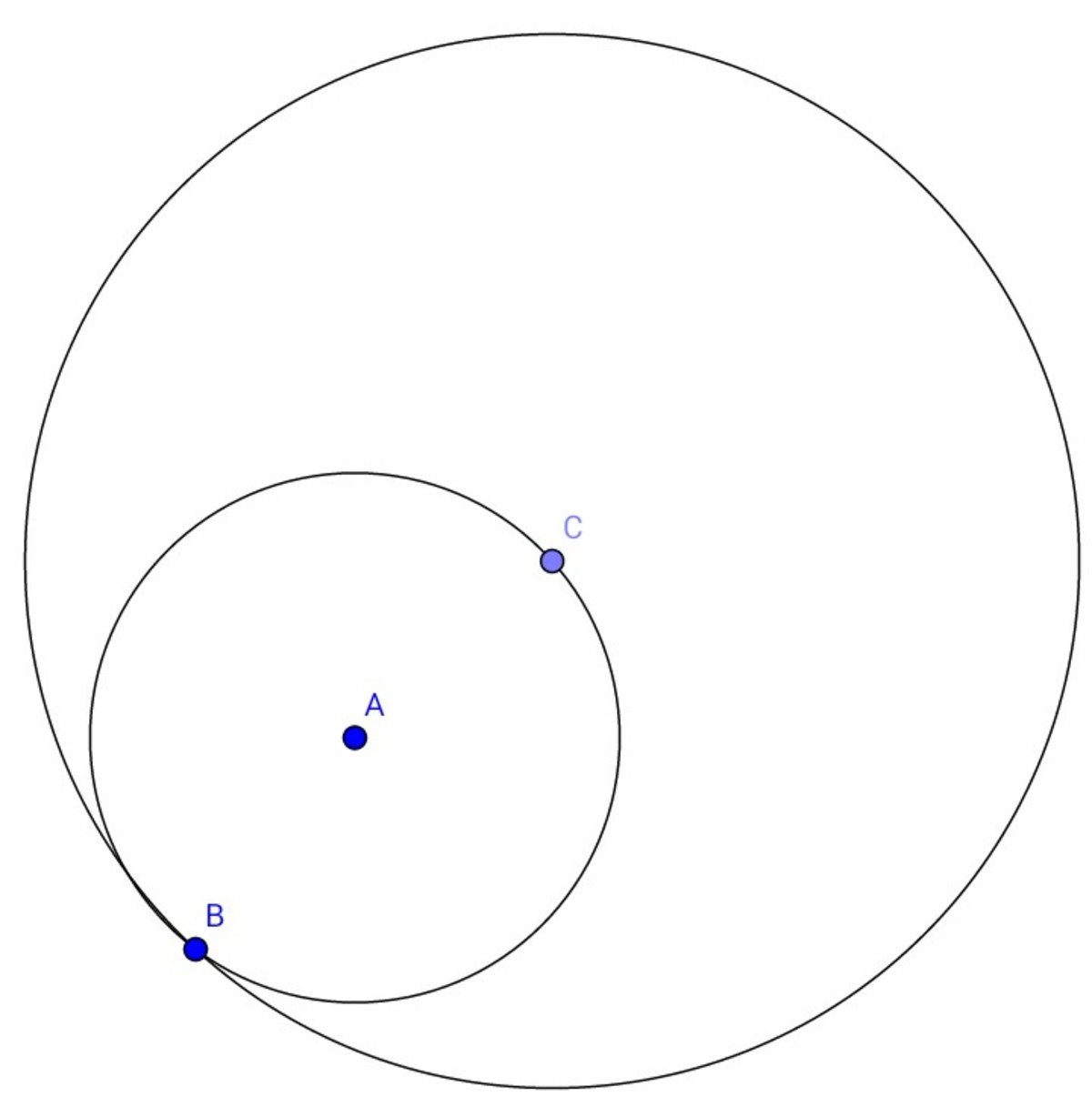

In the last figure the circle A is completely inside the circle C, and in that case radius of circle C becomes equal to diameter of circle A

Radius of circle C= diameter of circle A= 20 20

Diameter of circle C=2× Radius of circle C= 40 \boxed{40}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Exactly, the figure looks just like A is a subset of B. Great question! For circle B to encircle circle A, the radius of B should be equal to the diameter of A when B lies on the circumference of A. So, the diameter of circle B would be 4×10 = 40

Ashish Menon - 5 years, 1 month ago

Log in to reply

Thanks a lot, I will try to make some more questions. :)

Abhay Tiwari - 5 years, 1 month ago

Here you go

Abhay Tiwari - 5 years, 1 month ago

Log in to reply

Great question, posting a solution right away #claps #whistles

Ashish Menon - 5 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...