Only important clue

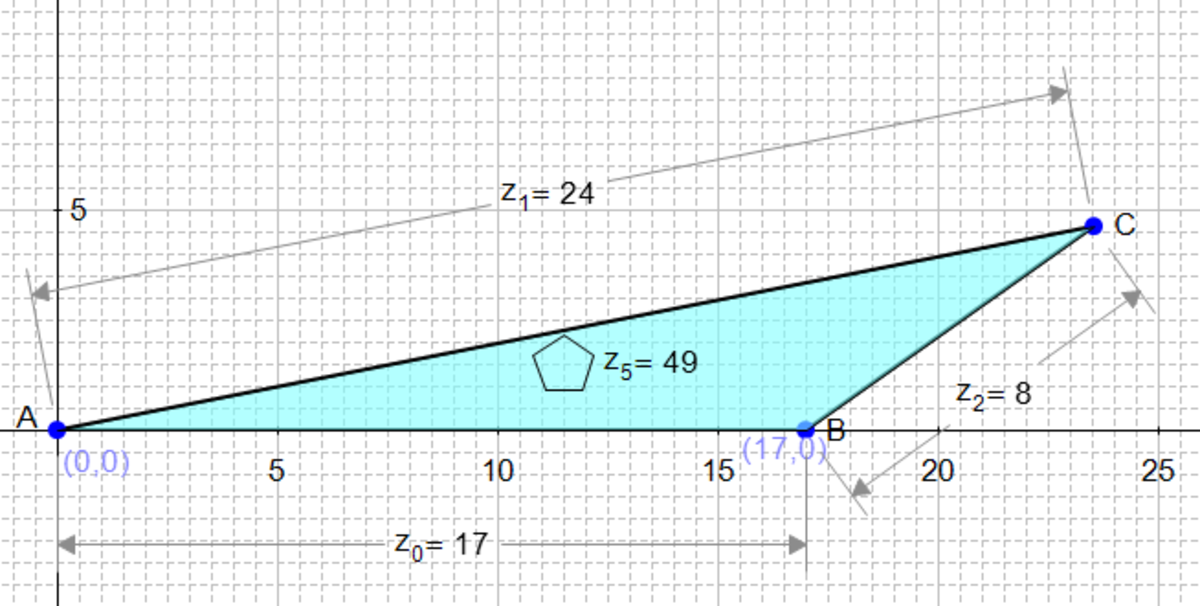
By the triangle inequality, (assuming we are looking for non-degenerate triangles), we require that $x + 17 \gt 3x \Longrightarrow \dfrac{17}{2} \gt x.$

Since $x$ must be an integer, the greatest integer value for $x$ is $8.$ The side lengths of the triangle with maximum perimeter are then $8, 24, 17,$ giving a perimeter of $\boxed{49}.$

x+17>3x 2x<17 8,24,17

$x+3x > 17 \Rightarrow x \geq 5$

$x+17 >3x \Rightarrow x \leq 8$

For maximum perimeter, sides need to be $8,24,17$

Hence perimeter is $49$