Semicircle inception
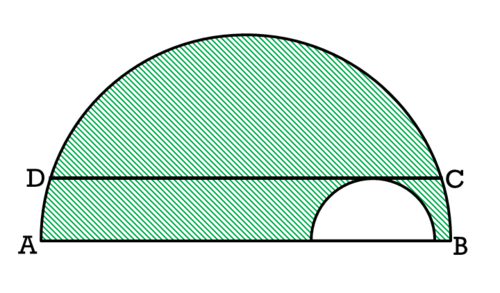 If the shaded area is
x
π
,
give the value of
x
.
If the shaded area is
x
π
,
give the value of
x
.
CD is a chord of length 16 parallel to the diameter AB and the small semicircle is tangent to the given chord.
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
thanks! calvin sir
That is area of half of the circle that you created. Not the shaded part :p
Log in to reply
He did not create any circle.
Let R be the radius of the larger circle, and r be the radius of the smaller circle. Then, the area of the shaded part is 2 π ( R 2 − r 2 ) .
Rudresh shows that R 2 − r 2 = 6 4 , which is substituted into the above area equation.
What does x represent? The area of shaded region is 32 pi square units.
Thanks for the solution .
nice one..
FYI - To display images in the solution, you can use the markdown code of

If you're already hyperlinking to the image url, then just add a ! in front of it.
I edited your solution, so that you can refer to it. Great diagram BTW.
power of point worked as well!
Let R be the radius of the big circle and r be the small circle's radius,now CD=16,and half of CD is 8.Now R^2-r^2=8^2=64.the shaded region is (pi R^2)/2-(pi r^2)/2=pi/2(R^2-r^2)=pi/2 (8)^2=pi 32=32*pi.So x=32
Thanks for the solution .
We assume that this problem holds true for all pairs (R, r) which satisfy the above conditions, where R is the radius of the large semicircle, and r is the radius of the small semicircle. We then choose (R, r) = (16/2, 0), which is clearly a solution. The area of the resulting semicircle is 1/2 pi 8^2 = 32pi.
Is this okay?
Let r be the radius of the big semicircle and j be the radius of the small semicircle. By power of a point, we see that (r-j)(r+j) = 8*8, so r 2 − j 2 = 6 4 . Note that we want x such that x π = π / 2 ( r 2 − j 2 ) , so the answer is x = 3 2 .
I n △ D E F , R 2 = 8 2 + r 2 ⇒ R 2 − r 2 = 6 4 a r ( s h a d e d p a r t ) = 2 π [ R 2 − r 2 ] ⇒ 2 π [ 6 4 ] = 3 2 π s o x = 3 2