A geometry problem by Adrian Gonzalez
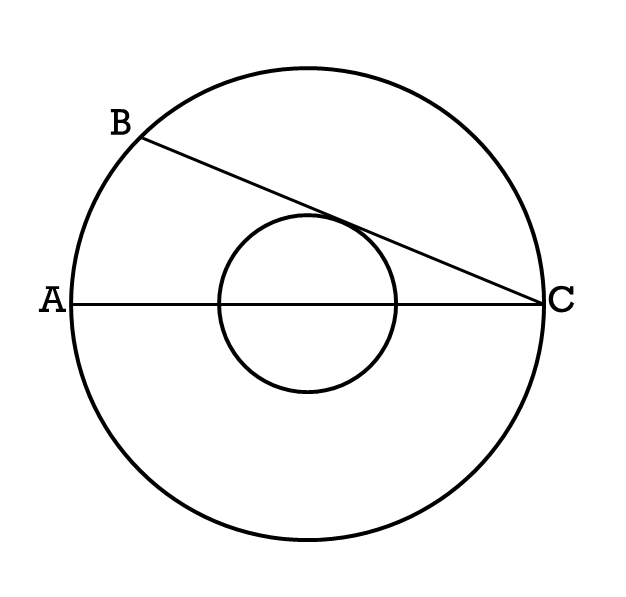 The ratio of the radii of two concentric circumferences is 1:3. If
AC
is a diameter of the largest circle,
BC
is a chord of the larger circle that is tangent to the small circle and
AB
= 18, What is the radius of the larger circle?
The ratio of the radii of two concentric circumferences is 1:3. If
AC
is a diameter of the largest circle,
BC
is a chord of the larger circle that is tangent to the small circle and
AB
= 18, What is the radius of the larger circle?
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
dices que x es el radio del circulo pequeño, pero si fuera similar a AB, entonces no seria el radio, sino un arco... entonces estaria mal
how are the triangles ABC & OPC similar
Let the point of tangency between chord B C and the smaller circle be point P , and the center of the circle (it doesn't matter which one, as they are concentric) be point O . Now, consider Δ O P C and Δ A B C . Note that ∠ O P C = ∠ A B C = 9 0 , and ∠ C = ∠ C . Thus, the triangles are similar by AAA. Now, note that A C = 2 ⋅ O C . Thus, the scale factor between the triangles is 2 . Now, since A B = 1 8 , we have O P = 2 A B = 2 1 8 = 9 . Thus, the radius of the smaller circle is 9 . Since the ratio of the smaller radius to the larger radius is 1 : 3 , we see that the radius of the larger circle is 9 ⋅ 3 = 2 7 .
Let O b center point and P be the point on small circle wher tangent touches. join line AB & OP both triangle are similar hence OP=1/2 AB AB=18 then OP=9 OP is radius of smaller circle hence smaler circle radius is 9 thn larger circel radius is 3xsmaller circle radius 3 x 9 27 Answer.
Let O be the center of the two circles and let P be the point of tangency of B C with the smaller circle.
Now let x be the radius of the smaller circle, (and thus 3 x the radius of the larger circle). Then triangles A B C and O P C are similar right triangles. So we thus have that
A C A B = O C O P ⟹ 6 x 1 8 = 3 x x ⟹ x = 9 .
The radius of the larger circle is thus 3 x = 2 7 .