Tight Packing Shapes
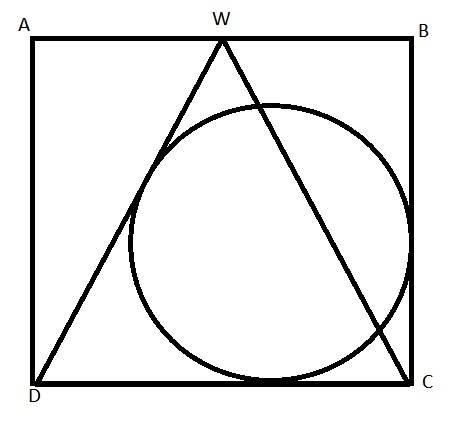
In the figure above, A B C D is a square with side length 16 and W is the midpoint of A B . Find the radius of the circle to two decimal places.
The answer is 6.11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
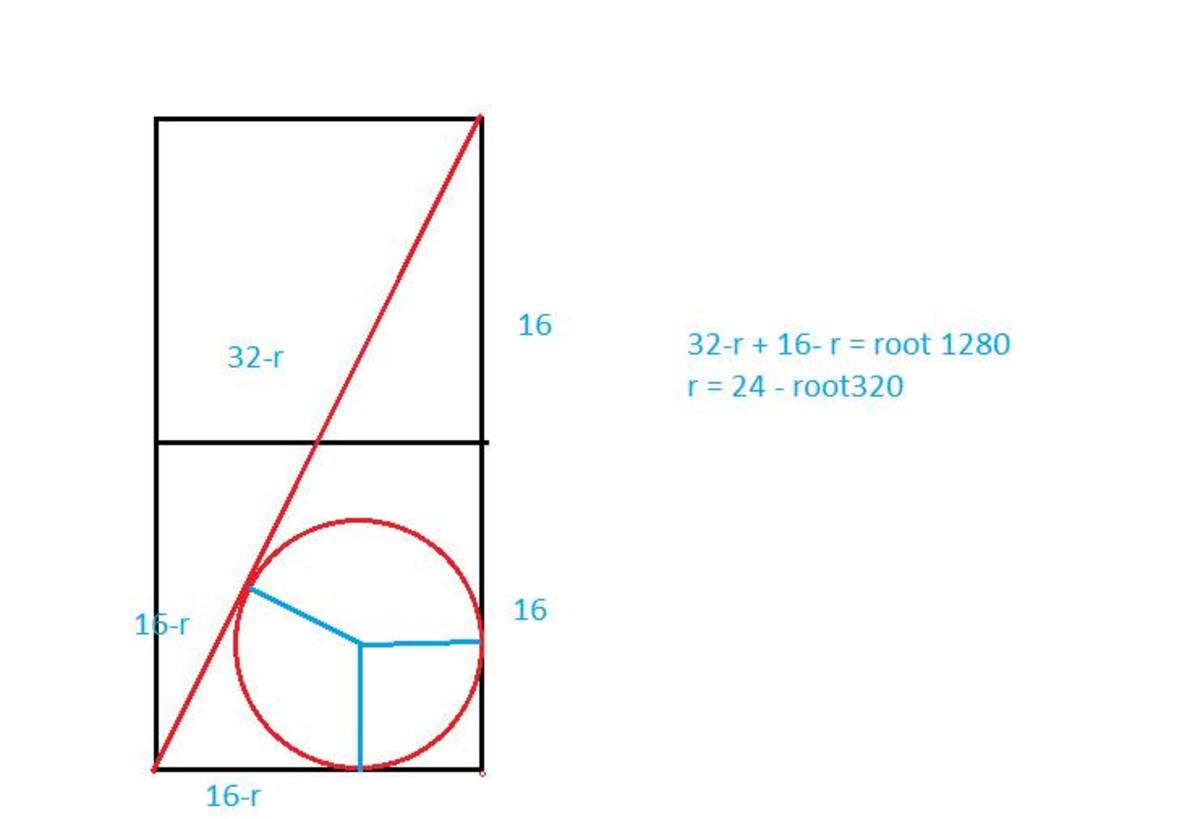
Very good question I got the ans using same method
this one i gonna be the easiest one ...
Log in to reply
Indeed. Very clever. :)
sir how have you modified the figure????
What a delight! Brilliant!
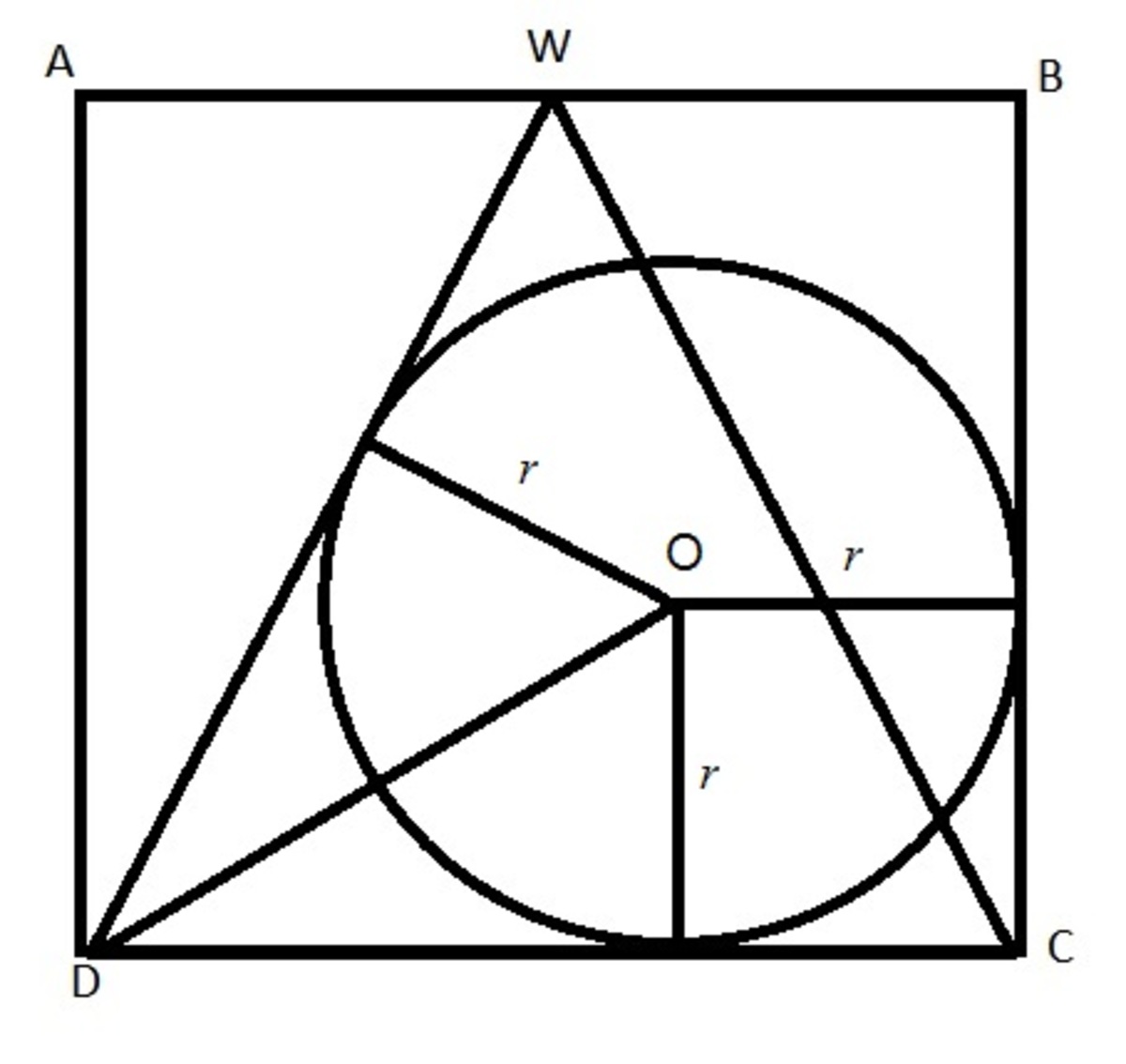
Let ∠ W D C = θ , then tan θ = 8 1 6 = 2 . Let O be the centre and r be the radius of the circle. Then we note that ∠ O D C = 2 θ . Then we have tan 2 θ = 1 6 − r r . Using a calculator, we can find θ = 1 . 1 0 7 1 4 8 7 1 8 rad , then tan 2 θ = 0 . 6 1 8 0 3 3 9 8 9 and r = 6 . 1 1 1 4 5 6 1 8 ≈ 6 . 1 1 .
Using hand calculations is as follows:
tan θ 1 − tan 2 2 θ 2 tan 2 θ 1 − ( 1 6 − r ) 2 r 2 2 ⋅ 1 6 − r r 2 5 6 − 3 2 r + r 2 − r 2 1 6 r − r 2 1 6 r − r 2 r 2 − 4 8 r + 2 5 6 ⟹ r = 2 = 2 = 2 = 1 = 2 5 6 − 3 2 r = 0 = 2 4 ± 8 5 = 2 4 − 8 5 ≈ 6 . 1 1 Note that tan 2 θ = 1 6 − r r As 2 4 + 8 5 > 1 6 , it is rejected.
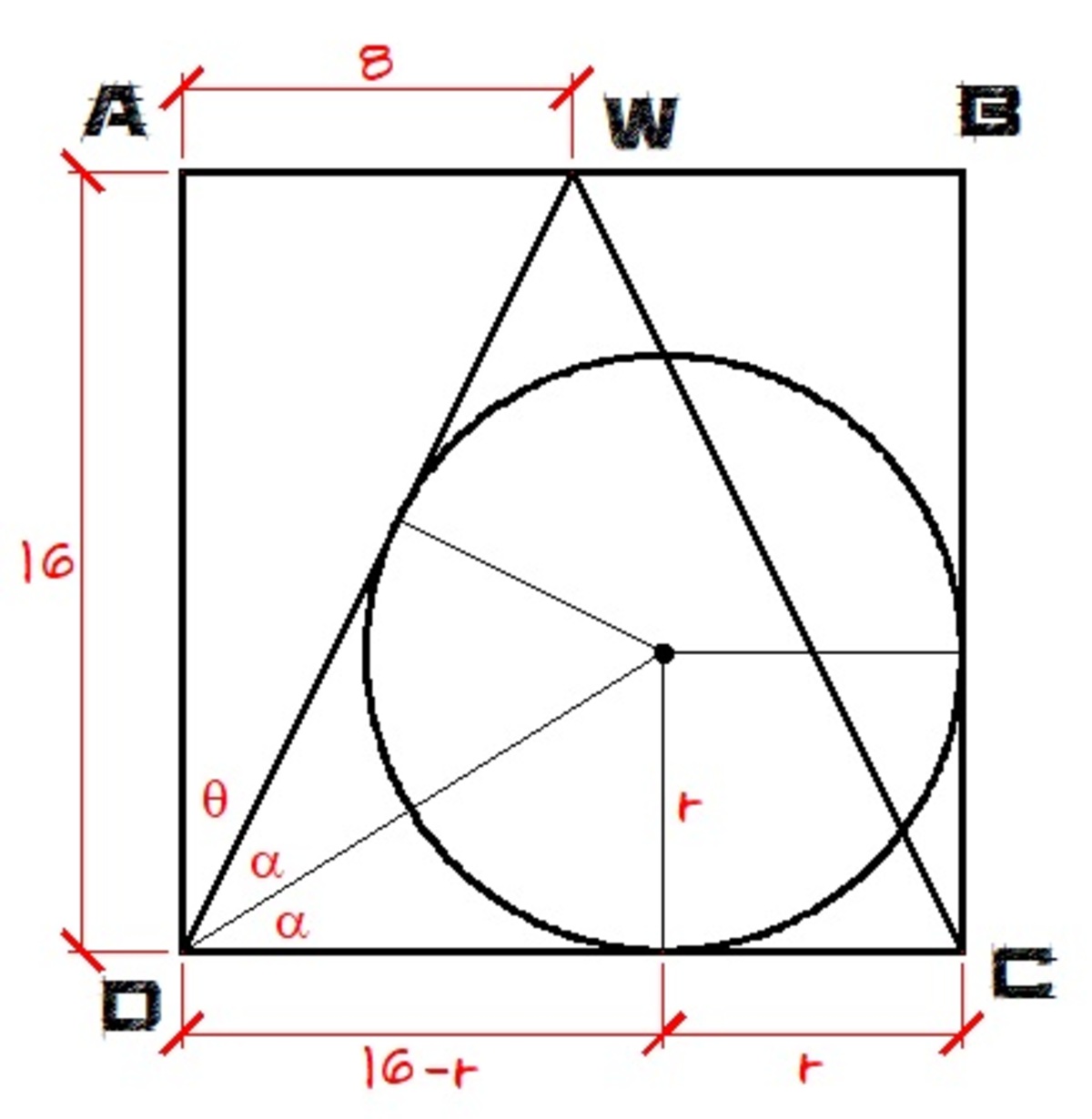 Using trigonometry.
Using trigonometry.
tan θ = 1 6 8 ⟹ θ = tan − 1 ( 1 6 8 ) ≈ 2 6 . 5 6 5
α = 2 9 0 − 2 6 . 5 6 5 ≈ 3 1 . 7 1 7 5
Then,
tan 3 1 . 7 1 7 5 = 1 6 − r r
9 . 8 8 9 − 0 . 6 1 8 = r
1 . 6 1 8 r = 9 . 8 8 9
r ≈ 6 . 1 1