A geometry problem by Ajay Sutradhar
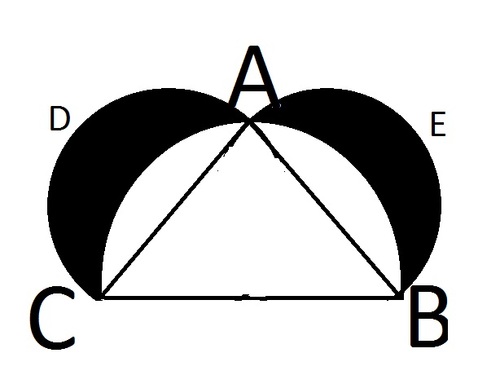 ABC is semicircle, where A is any point on the semicircle. Taking AB and AC as diameter two more semicircles are formed. what is the ratio between the area of shaded portion to that of the area of the triangle ABC.
ABC is semicircle, where A is any point on the semicircle. Taking AB and AC as diameter two more semicircles are formed. what is the ratio between the area of shaded portion to that of the area of the triangle ABC.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
The solution posted by ajay is totally correct but it may be confusing as he hasn't used proper formatting guide tools.....
So here's my answer.....
Since, CB is the diameter of the biggest circle, it will make 90* at the point of contact to the circle....
(since angle subtended by the diameter of a circle to its circumference is always 90*)
Therefore, angle CAB = 90*
Take CA= q ; AB = r and CB = p
Therefore according to Pythagoras theorem:
C B 2 = A C 2 + A B 2
p = q+r .................................eq.1
If you watch closely, AREA OF THE SHADED PORTION can be calculated by:
area of circle CDA + area of circle BEA + area of triangle CAB - area of circle CAB
=[ 2 1 X π X 4 A C 2 ] + [ 2 1 X π X 4 A B 2 ] + [ 2 1 X BA X AC] - [ 2 1 X π X 4 B C 2 ]
=[ 2 1 X π X 4 q ] + [ 2 1 X π X 4 r ] + [ 2 1 X r X q ] - [ 2 1 X π X 4 p ]
= 2 1 X [π X 4 q + π X 4 r + r q - π X 4 p ]
= 2 1 X [π X 4 q + π X 4 r + r q - π X 4 r + q ]
= 2 1 X [π X 4 q - π X 4 q + π X 4 r - π X 4 r + r q ]
= 2 1 X r q ....................... eq.2
Therefore ratio of area of shaded portion to that of area of the triangle is:
= 2 1 X r q : 2 1 X r q
Therefore the ratio is 1 : 1
I have my own modified version of the solution that I want to share If you get the Area of Semi Circle D and add it to the Area of semi circle E Then Subtract ( The area of semi circle CAB - Area of the triangle) You get the area of the shaded Part. Also adding to what Jaiveer Shekhawat said, You don't have to involve with direct variable naming here. Since we know that angle CAB is 90 degrees like he explained then Angle ACB = Angle ABC = 45 degrees. That said, The triangle 45,45,90 is a VERY FAMOUS triangle where the two sides opposite to the 45 degrees angles is of length (1) and the hypotenuse opposite to the 90 degrees angle is (root 2). That said you can easily get its area by doing: 1/2 x 1 x 1 = 1/2 So the triangle's area is 1/2 Next We know length AC = AB = 1 as we said before since is is in a 45,45,90 triangle. Therefore the radius of semi circle D is 1/2 and the radius of semi circle E is 1/2 also. The 2 areas combined are: 2 x (1/2 x pi x (1/2)^2) = 2 x (1/2 x pi x 1/4) = 1/4 pi Therefore the area of both Semi circles (D) and (E) combined are 1/4 pi Finally, we know that CB = root 2 since it is the hypotenuse of a 45,45,90 angle therefore the area of the semi circle CAB = 1/2 x pi x (root 2/2)^2 = 1/4 pi Finally we have all what we need to solve the equation: Area of Semi circle D + E = 1/4 pi Area of semi circle CAB = 1/4 pi Area of triangle CAB = 1/2
Now to get the ratio of Area of shaded area to Area of the triangle we use this formula:
[Area of semi circles D & E -( Area of semi circle CAB - Triangle CAB) ]/ [ Area of triangle CAB ] = 1/4 pi - (1/4 pi - 1/2) / 1/2 = 1/4 pi - 1/4 pi + 1/2 / 1/2 = 1/2 / 1/2 = 1 Therefore the ratio is 1:1 Please ask if you need me to clarify anything :)
sorry farouk, it is not necessarily 45,45,90 triangle. its just a right angled triangle. it is no where mentioned that AB=AC or angleC is equal to angle B.
Log in to reply
Sorry I just saw this now :) here is my response: It says in the question: "where A is any point on the semicircle. " So I assumed without loosing generality that the point is in the exact middle therefore by similarity angle ACB = CAB = (180-90)/2 = 45
Using the fact that point A is any point on the semicircle.Suppose POINT A is at point C. Thus AC is zero and CB=AB. Hence two circles have same diameters i.e. same area. Hence ratio is 1:1.
Let x be half the length from C to B
The area of the triangle is simply equal to x 2
The area of the semicircle bounded by A B C is equal to \(\frac{𝜋x^{2}}{2}\)
The unshaded area of the two semicircles D and E is equal to the area of the semicircle bounded by A B C minus the area of the triangle \(\frac{𝜋x^{2}}{2}-x^{2}=\frac{(𝜋-2)x^{2}}{2}\)
The radius of the two semicircles D and E can be found by calculating half of the length from A to B using the Pythagorean Theorem 2 x 2 + x 2 = 2 2 x
The combined area of the two semicircles D and E is equal to \(𝜋(\frac{\sqrt{2}x}{2})^{2}=𝜋(\frac{2x^{2}}{4})=\frac{𝜋x^{2}}{2}\)
The shaded area of the two semicircles D and E is equal to \(\frac{𝜋x^{2}}{2}-\frac{(𝜋-2)x^{2}}{2}=\frac{(𝜋-𝜋+2)x^{2}}{2}=\frac{2x^{2}}{2}=x^{2}\)
The ratio between the area of the shaded portion and the area of the triangle is surprisingly equal to x 2 : x 2 = 1 : 1
Area of semi circle ABC=1/4πCB2 ;
Area of semi circle ADC=1/4πAC2;
AreaofsemicircleAEB= 1/4πAB2;
As triangle ABC is formed by a diameter of semicircle, so ABC is a righangled triangle Aplying Pythagorous theorem , CB2 =AB2+AC2;
1/4πCB2 =1/4πAB21/4πAC2
Hence, Area of semi circleABC=Area(ADC)+Area(AEB);
Ie,Area of triangleABC+Area of chord AC+Area formed by chord AB=Area of both shaded portion+Area formed by ChordAB+Area formed by Chord AC;
Ie, Area of triangle ABC=Area of total shaded portion;
Hence the ratio is 1:1