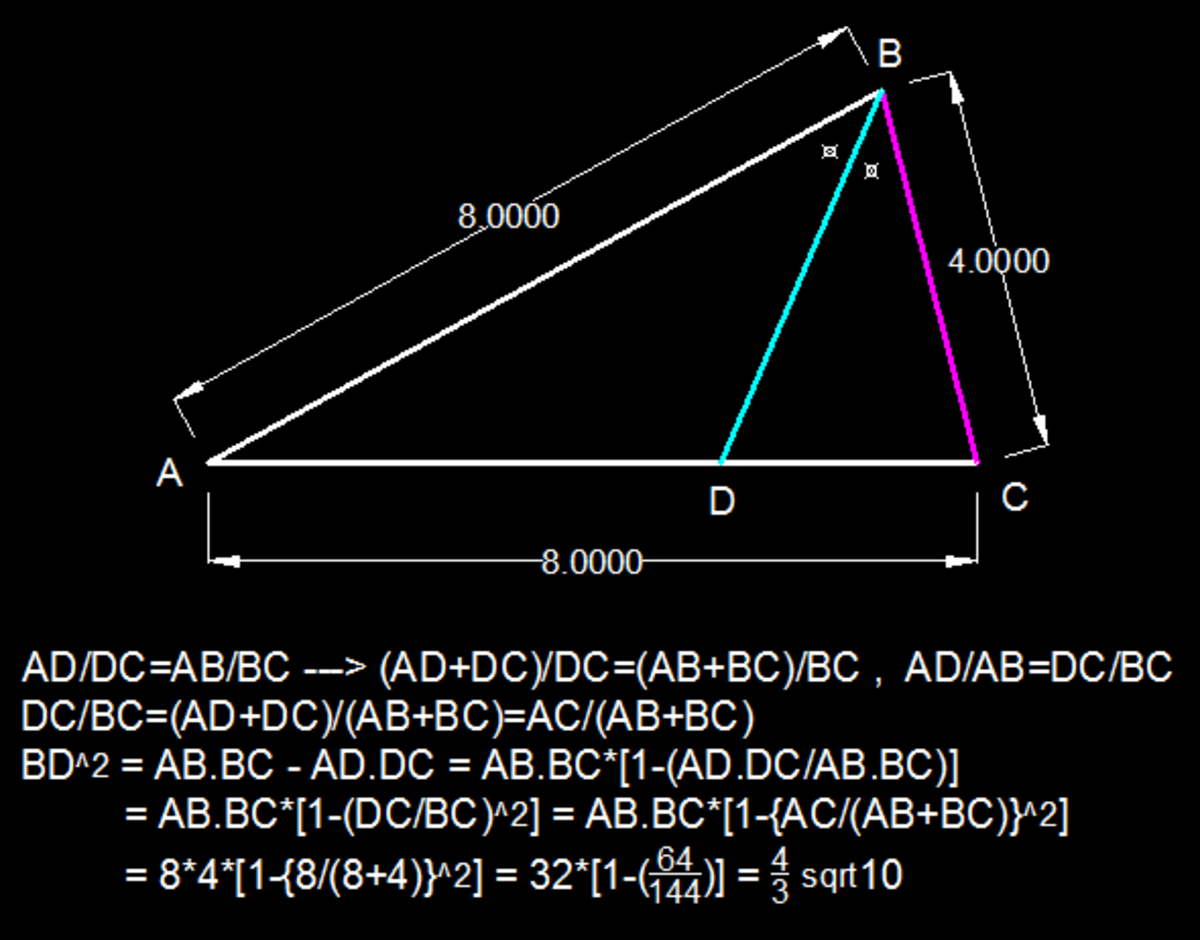
A geometry problem by Akshat Sharda
A triangle of side 8,8 and 4 has a angle bisector to side of length 8. Find the length of the angle bisector.
If your answer comes as c a b with b square-free, submit your answer as the minimum value of a + b + c .
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
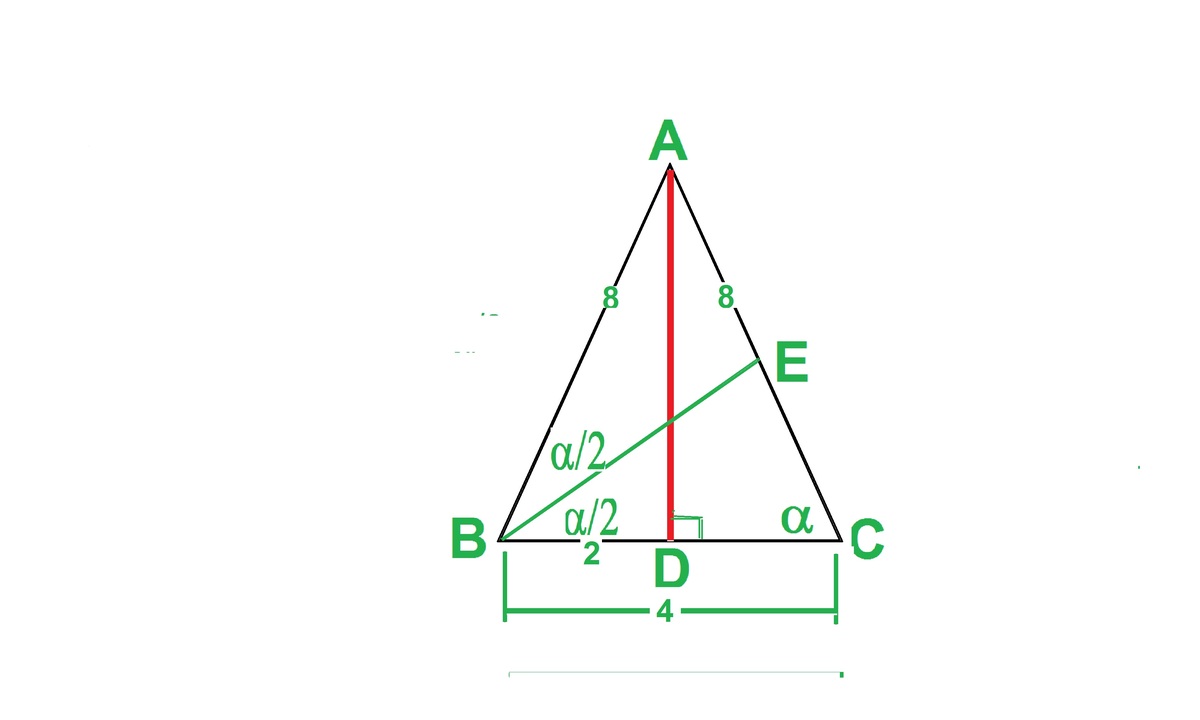 Let ABC be the triangle, AB=AC=8, BC=4.
A
D
a
l
t
i
t
u
d
e
o
f
I
S
O
S
C
E
L
E
S
Δ
.
B
E
t
h
e
a
n
g
l
e
b
i
s
e
c
t
o
r
.
C
o
s
α
=
8
2
=
4
1
.
∴
b
y
t
r
i
.
f
o
r
m
u
l
i
i
,
S
i
n
α
=
4
1
5
,
S
i
n
2
α
=
8
3
,
C
o
s
2
α
=
8
5
∴
S
i
n
(
α
+
2
α
)
=
S
i
n
α
∗
C
o
s
2
α
+
C
o
s
α
∗
S
i
n
2
α
=
4
2
3
3
.
.
.
(
∗
∗
)
Applying Sin Law in
Δ
E
B
C
,
S
i
n
α
B
E
=
S
i
n
C
E
B
4
=
(
∗
∗
)
4
∴
B
E
=
4
1
5
∗
4
2
3
3
4
=
3
4
∗
1
0
=
c
a
∗
b
∴
a
+
b
+
c
=
1
7
Let ABC be the triangle, AB=AC=8, BC=4.
A
D
a
l
t
i
t
u
d
e
o
f
I
S
O
S
C
E
L
E
S
Δ
.
B
E
t
h
e
a
n
g
l
e
b
i
s
e
c
t
o
r
.
C
o
s
α
=
8
2
=
4
1
.
∴
b
y
t
r
i
.
f
o
r
m
u
l
i
i
,
S
i
n
α
=
4
1
5
,
S
i
n
2
α
=
8
3
,
C
o
s
2
α
=
8
5
∴
S
i
n
(
α
+
2
α
)
=
S
i
n
α
∗
C
o
s
2
α
+
C
o
s
α
∗
S
i
n
2
α
=
4
2
3
3
.
.
.
(
∗
∗
)
Applying Sin Law in
Δ
E
B
C
,
S
i
n
α
B
E
=
S
i
n
C
E
B
4
=
(
∗
∗
)
4
∴
B
E
=
4
1
5
∗
4
2
3
3
4
=
3
4
∗
1
0
=
c
a
∗
b
∴
a
+
b
+
c
=
1
7
Great solution ^_^ U p v o t e d !
For solving this,
We have a great formula , M a = b + c 2 b × c × s ( s − a )
Where :
M a = Median to side a .
s = Semi-perimeter.
Let , a = b = 8 and c = 4
Therefore ,
⇒ M a = 8 + 4 2 8 × 4 × 1 0 × 2
⇒ M a = 1 2 1 6 1 0 = 3 4 1 0
Nice formula. Any formula for length of angle bisector?
Log in to reply
Actually that was the formula for the angle bisector.
As Alan Enrique Ontiveros Salazar points out M a is angle bisector. Please correct.