Of Cones and Spheres
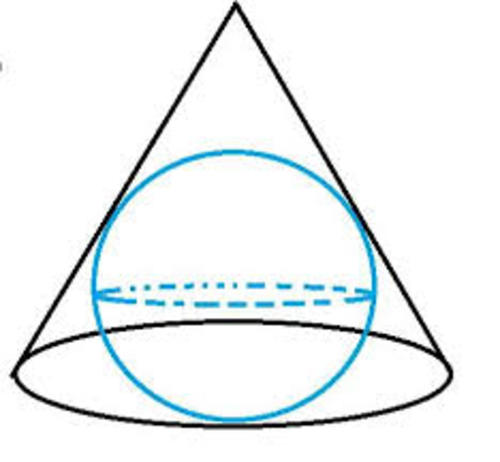 There is a cone.The slant height of cone is 6√3 and radius is 3√3. There is a sphere inscribed in the cone(touching its base and curved surface). Find the radius of sphere.
There is a cone.The slant height of cone is 6√3 and radius is 3√3. There is a sphere inscribed in the cone(touching its base and curved surface). Find the radius of sphere.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
 sin
θ
=
6
3
3
3
=
2
1
⟹
θ
=
3
0
sin
θ
=
6
3
3
3
=
2
1
⟹
θ
=
3
0
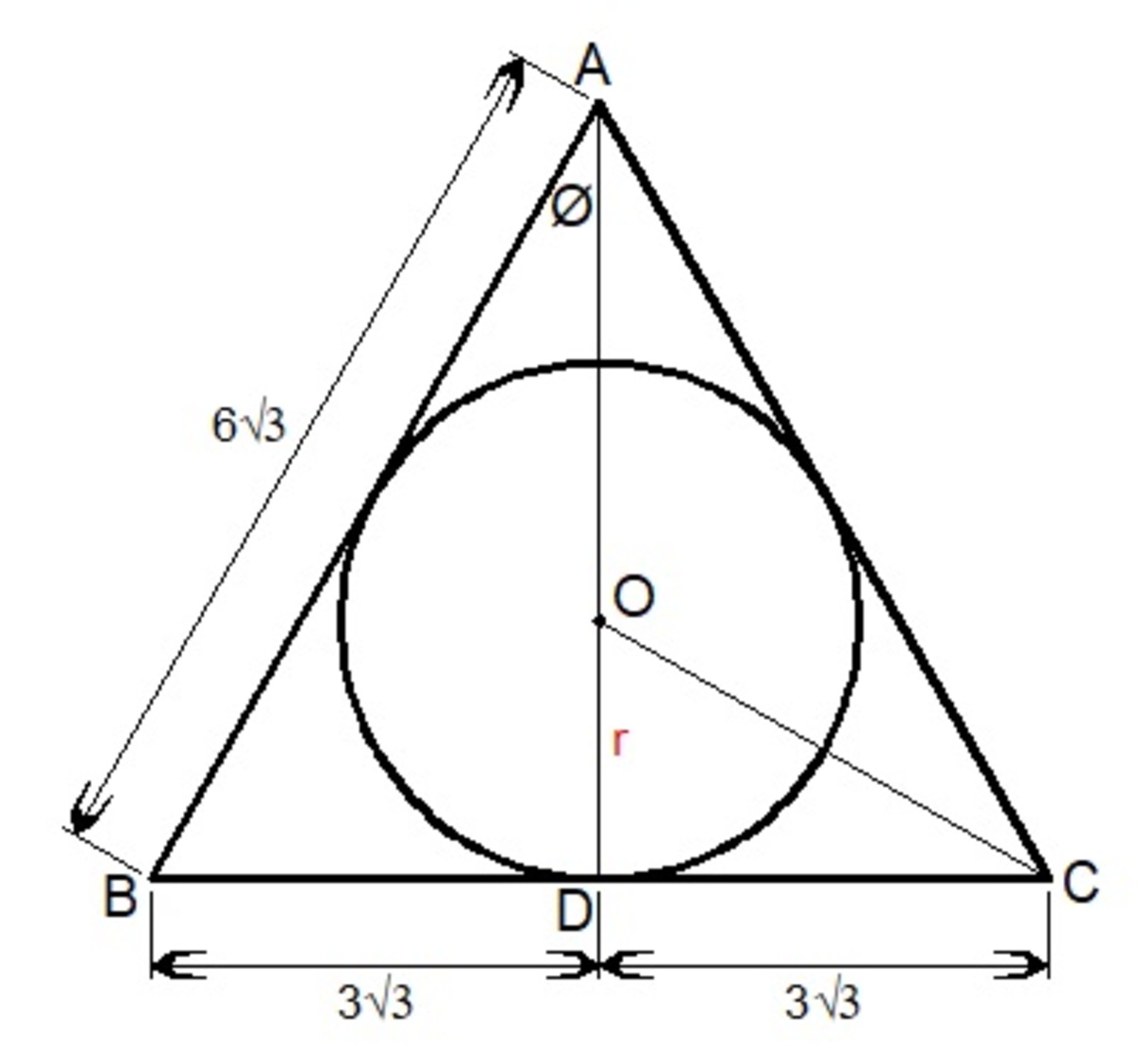
It means that the 2-dimensional view of the cone is an equilateral triangle. So ∠ D C O = 3 0 .
tan ∠ D C O = 3 3 r ⟹ r = tan 3 0 ( 3 3 ) ⟹ r = 3
by ratio and proportion: 1/2(9-r) = r r = 3
Firstly, imagine the shapes on a 2d plane (i.e. you're looking at them from the front). The sphere will be an incircle and the cone will be an equilateral triangle of side 6 3 . The area of the triangle = A t = 9 × 3 ( 3 ), semi-perimter = s = 9 3 . Now the radius of the incircle = r = s A t = 3 (by cancelling out common factors on the numerator and denominator) = radius of sphere