Octa - Gone!
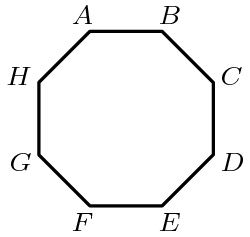
A regular octagon, A B C D E F G H has an area of 1 square unit. What is the area of the rectangle A B E F ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
Very nice observation regarding the different relations of the area of a regular polygon!
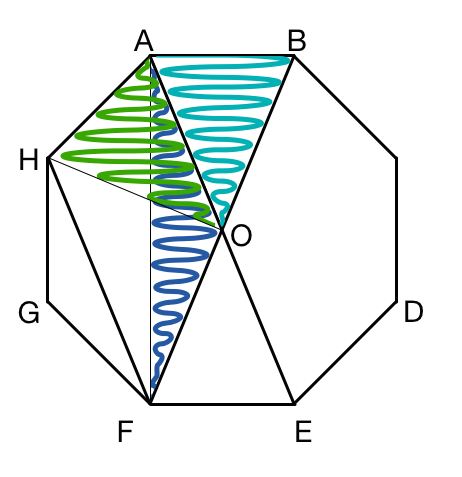
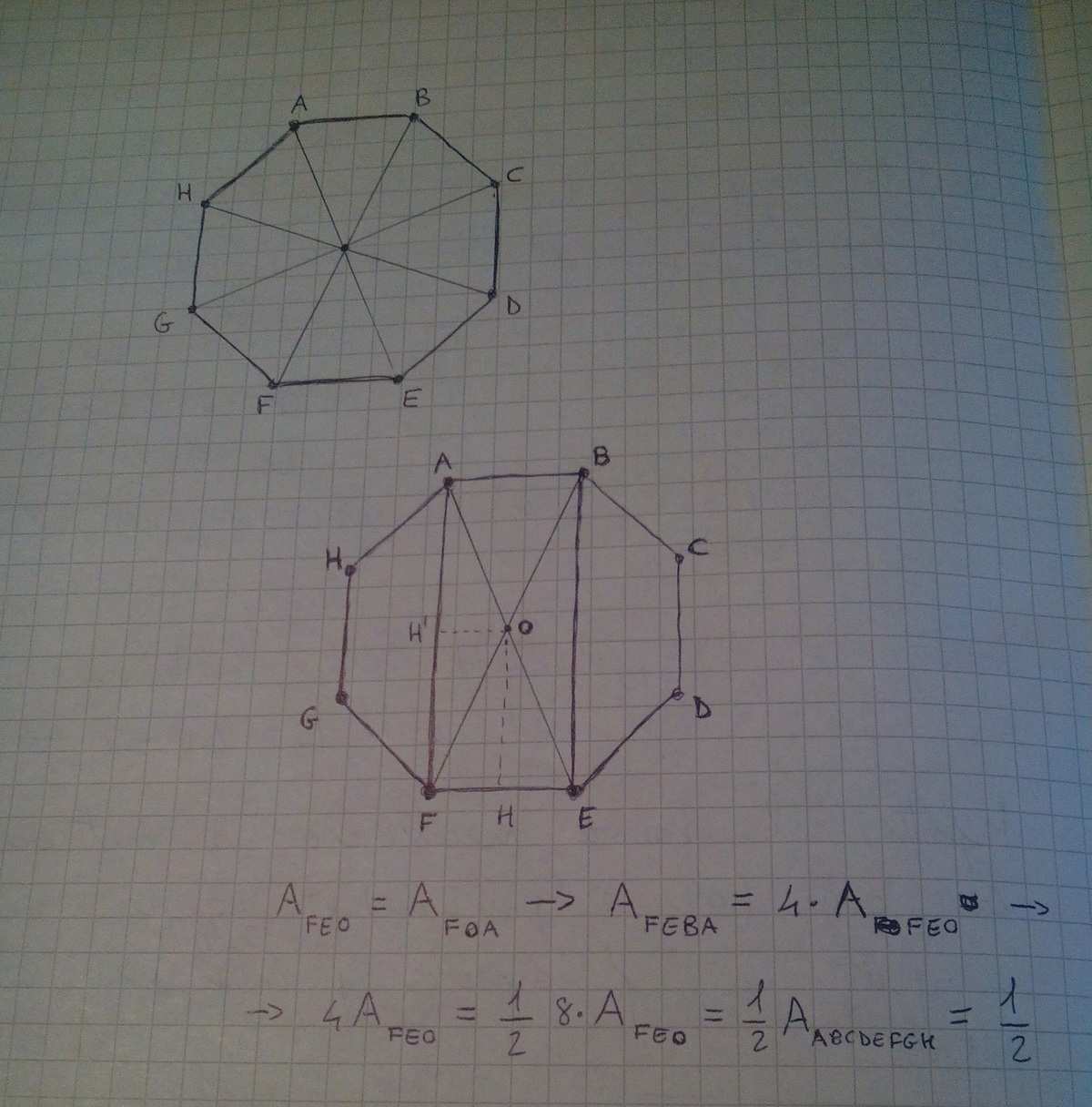
The octagon is formed by 8 isosceles triangles of the form OAB and OAH.
Consider triangle OAF. Since
A
O
E
∥
H
F
, by considering base
A
O
and point the point
F
in a parallel manner, we see that
[
O
A
F
]
=
[
O
A
H
]
(Alternatively, these triangles have the same base
O
A
and the same height).
Similarly, we see that
[
O
B
F
]
is equal to one of these isosceles triangles.
Thus, [ A B E F ] comprises 4 isosceles triangles, hence the area is half that of the octagon.
I found this result really surprising, and was looking for a more intuitive / non-calculation-intensive approach.
Relevant wiki: Regular Polygons - Problem Solving - Medium
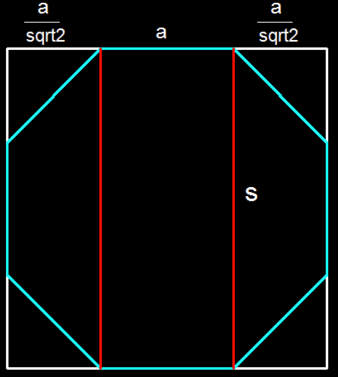 Area of the four edged triangles is
4
⋅
2
1
(
2
a
)
2
=
a
2
.
Area of the four edged triangles is
4
⋅
2
1
(
2
a
)
2
=
a
2
.
Area of a regular octagon is
s
2
−
a
2
.
s
=
a
(
1
+
2
2
)
=
a
(
1
+
2
)
s
2
=
a
2
(
3
+
2
2
)
Area of regular octagon is
2
(
1
+
2
)
a
2
=
1
.
a 2 = 2 ( 2 + 1 ) 1
Area of rectangle is
a
×
s
=
2
(
2
+
1
)
1
⋅
(
2
+
1
)
=
2
1
.
Call the centre of the octagon O. The octagon is made up of 16 congruent triangles from O to the midpoint of each side and a vertex. ABEF is made up of 8 of these triangles so (8/16)*1=0.5
Hm, how do you see that "ABEF is made up of 8 of these triangles"?
Log in to reply
call the midpoint of BE, "M" and the midpoint of FE, "N". Now obviously, by definition, NOE is one of the triangles and it can be shown NOE and MOE lie within a rectangle so by SAS NOE and MOE are congruent and similar things can be said for the other four cases so there are eight in total.
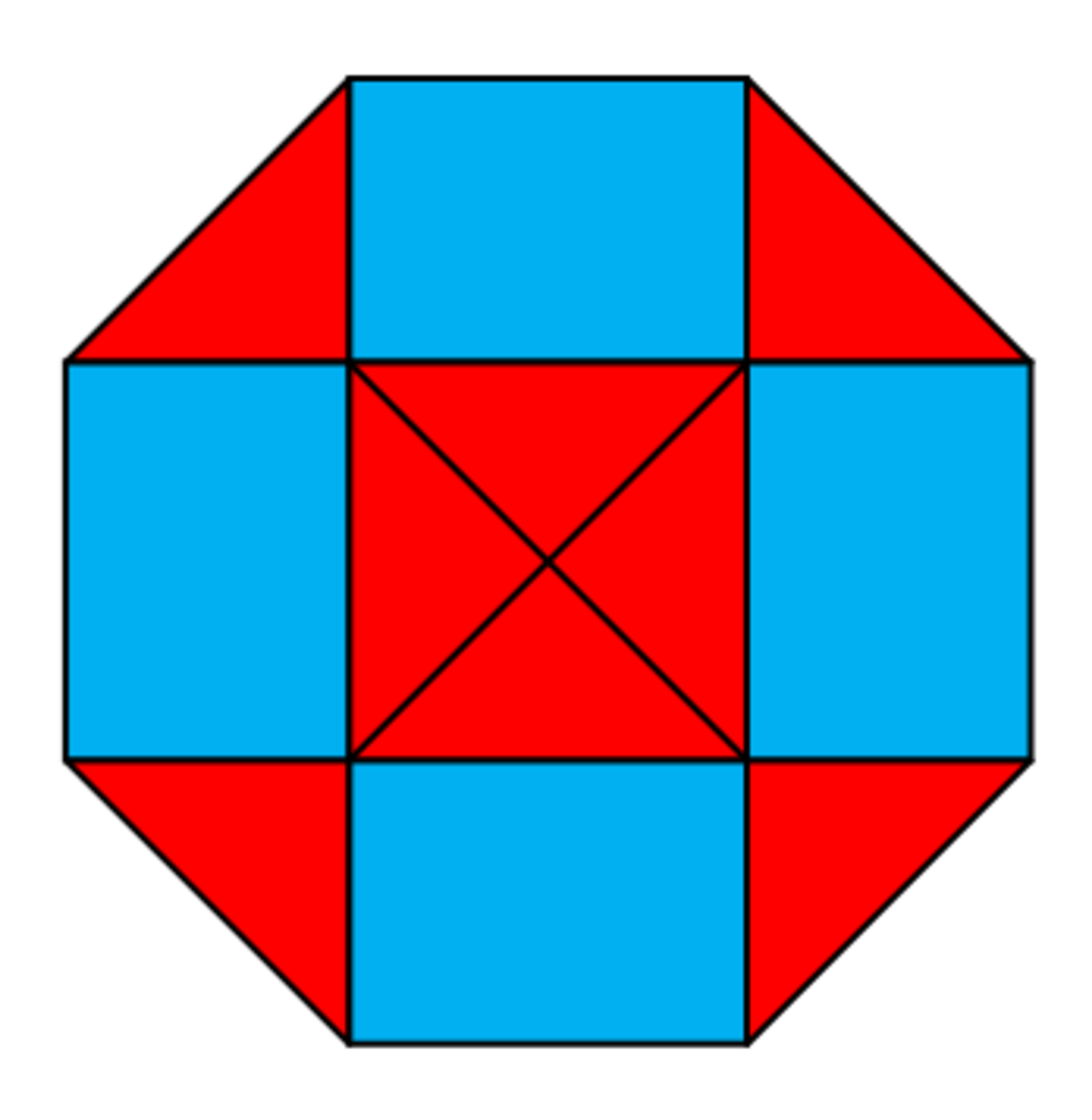
Relevant wiki: Regular Polygons - Area
If the side length of the octagon is s and the apothem(perpendicular distance from the centre to the side of the octagon) is a , the area of the rectangle A B E F will be 2 a s .
And the area of the octagon is given as 1.
∴ 1 = 2 8 a s ⇒ 2 a s = 2 1 .
Hence the area of the rectangle A B E F is 2 1 . □