Welcome 2016! Part 13
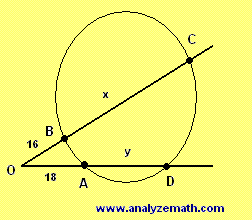 In the figure above,
△
O
A
B
has an area of 72 and
△
O
D
C
has an area of 288. Find
x
+
y
.
In the figure above,
△
O
A
B
has an area of 72 and
△
O
D
C
has an area of 288. Find
x
+
y
.
The answer is 34.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Beautiful, simple, up voted.
C O ∗ O B = D O ∗ O A ⟹ ( x + 1 6 ) ∗ 1 6 = ( y + 1 8 ) ∗ 1 8 . . . . . . . . . . . . ( A ) ∴ y + 1 8 = ( x + 1 6 ) ∗ 9 8 . A r e a Δ O D C A r e a Δ O A B = ( x + 1 6 ) ( y + 1 8 ) 1 6 ∗ 1 8 = 2 8 8 7 2 = 4 1 . . . . . . . . . . ( B ) ∴ y + 1 8 = 4 ∗ 1 6 ∗ 1 8 ∗ x + 1 6 1 . ⟹ ( x + 1 6 ) ∗ 9 8 = 4 ∗ 1 6 ∗ 1 8 ∗ x + 1 6 1 , ⟹ ( x + 1 6 ) 2 = 8 4 ∗ 1 6 ∗ 1 8 ∗ 9 = 1 6 ∗ 8 1 . ∴ x + 1 6 = 4 ∗ 9 , ⟹ x = 2 0 . S u b s t i t u t i n g i n ( A ) 3 6 ∗ 1 6 = ( y + 1 8 ) ∗ 1 8 , ⟹ y = 1 4 . S o x + y = 3 4 .
A O B A = 2 1 ( 1 6 ) ( 1 8 ) ( sin ∠ C O D )
7 2 = 1 4 4 sin ∠ C O D
∠ C O D = 0 . 5
A O D C = 2 1 ( 1 6 + x ) ( 1 8 + y ) ( 0 . 5 )
1 1 5 2 = ( 1 6 + x ) ( 1 8 + y )
1 8 + y = 1 6 + x 1 1 5 2 ( 1 )
By the power of a point, we have
1 6 ( 1 6 + x ) = 1 8 ( 1 8 + y )
Substituting ( 1 ) , we have
1 6 ( 1 6 + x ) = 1 8 ( 1 6 + x 1 1 5 2 )
( 2 5 6 + 1 6 x ) ( 1 6 + x ) = 2 0 7 3 6
4 0 9 6 + 2 5 6 x + 2 5 6 x + 1 6 x 2 = 2 0 7 3 6
1 6 x 2 + 5 1 2 x − 1 6 6 4 0 = 0
x 2 + 3 2 x − 1 0 4 0 = 0
( X + 5 2 ) ( x − 2 0 ) = 0
x = − 5 2 or x = 2 0 reject the negative value
Solving for y , we have
1 8 + y = 1 6 + 2 0 1 1 5 2
1 8 + y = 3 2
y = 1 4
Finally,
x + y = 2 0 + 1 4 = 3 4
Typo 3rd line sin ∠ C O D .
S u b s t i t u t i n g ( 1 ) , w e h a v e 1 6 ( 1 6 + x ) = 1 8 ( 1 6 + x 1 1 5 2 ) ( 1 6 + x ) 2 = 1 6 1 8 ∗ 1 1 5 2 = 3 6 2 ⟹ 1 6 + x = 3 6 , ∴ x = 2 0 .
By cylic quad angles, ∠ O A B = ∠ O C D , and so, Δ O A B ∼ Δ O C D .
Then, it follows that: O C O A = O D O B = 2 8 8 7 2
1 6 + x 1 8 = 1 8 + y 1 6 = 2 1
Simple algebra yields x = 2 0 , y = 1 4 , so x + y = 3 4 .